Skip to contents

Generalized Hyperbolic Distribution

dist-gh.Rd

Density, distribution function, quantile function and random generation for the generalized hyperbolic distribution.

Usage

dgh(x, alpha = 1, beta = 0, delta = 1, mu = 0, lambda = -1/2, log = FALSE)
pgh(q, alpha = 1, beta = 0, delta = 1, mu = 0, lambda = -1/2)
qgh(p, alpha = 1, beta = 0, delta = 1, mu = 0, lambda = -1/2)
rgh(n, alpha = 1, beta = 0, delta = 1, mu = 0, lambda = -1/2)

Arguments

x, q

a numeric vector of quantiles.

p

a numeric vector of probabilities.

n

number of observations.

alpha

first shape parameter.

beta

second shape parameter, should in the range (0, alpha).

delta

scale parameter, must be zero or positive.

mu

location parameter, by default 0.

lambda

defines the sublclass, by default \(-1/2\).

log

a logical flag by default FALSE. Should labels and a main title drawn to the plot?

Details

dgh gives the density, pgh gives the distribution function, qgh gives the quantile function, and rgh generates random deviates.

The meanings of the parameters correspond to the first parameterization, pm=1, which is the default parameterization for this distribution.

In the second parameterization, pm=2, alpha and beta take the meaning of the shape parameters (usually named) zeta and rho.

In the third parameterization, pm=3, alpha and beta take the meaning of the shape parameters (usually named) xi and chi.

In the fourth parameterization, pm=4, alpha and beta take the meaning of the shape parameters (usually named) a.bar and b.bar.

The generator rgh is based on the GH algorithm given by Scott (2004).

Value

numeric vector

References

Atkinson, A.C. (1982); The simulation of generalized inverse Gaussian and hyperbolic random variables, SIAM J. Sci. Stat. Comput. 3, 502–515.

Barndorff-Nielsen O. (1977); Exponentially decreasing distributions for the logarithm of particle size, Proc. Roy. Soc. Lond., A353, 401–419.

Barndorff-Nielsen O., Blaesild, P. (1983); Hyperbolic distributions. In Encyclopedia of Statistical Sciences, Eds., Johnson N.L., Kotz S. and Read C.B., Vol. 3, pp. 700–707. New York: Wiley.

Raible S. (2000); Levy Processes in Finance: Theory, Numerics and Empirical Facts, PhD Thesis, University of Freiburg, Germany, 161 pages.

Author

David Scott for code implemented from R's contributed package HyperbolicDist.

Examples

## rgh -
   set.seed(1953)
   r = rgh(5000, alpha = 1, beta = 0.3, delta = 1)
   plot(r, type = "l", col = "steelblue",
     main = "gh: alpha=1 beta=0.3 delta=1")

 
## dgh - 
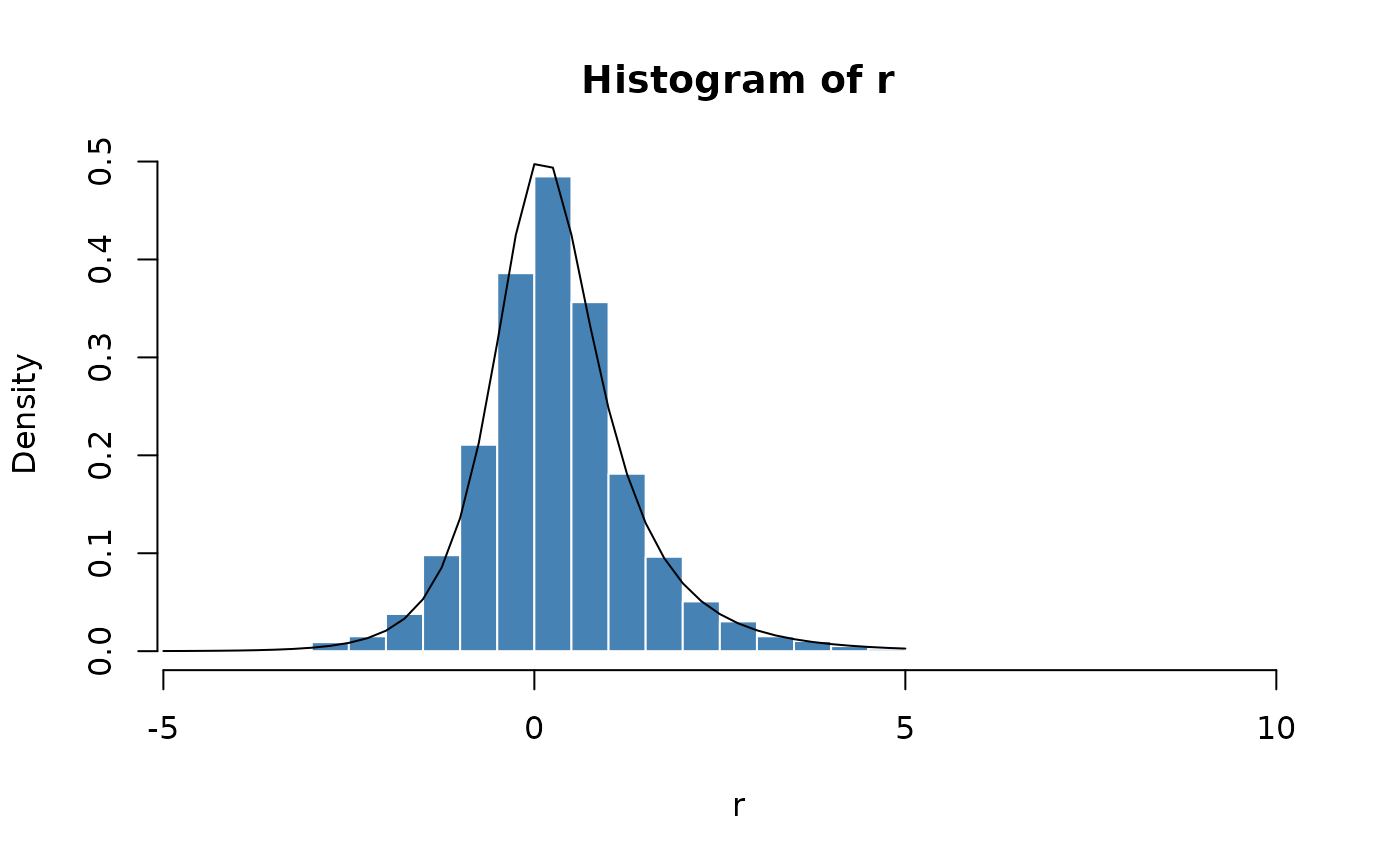
   # Plot empirical density and compare with true density:
   hist(r, n = 25, probability = TRUE, border = "white", col = "steelblue")
   x = seq(-5, 5, 0.25)
   lines(x, dgh(x, alpha = 1, beta = 0.3, delta = 1))

 
## pgh -  
   # Plot df and compare with true df:
   plot(sort(r), (1:5000/5000), main = "Probability", col = "steelblue")
   lines(x, pgh(x, alpha = 1, beta = 0.3, delta = 1))

   
## qgh -
   # Compute Quantiles:
   qgh(pgh(seq(-5, 5, 1), alpha = 1, beta = 0.3, delta = 1), 
     alpha = 1, beta = 0.3, delta = 1) 
#>  [1] -5.000001e+00 -4.000000e+00 -3.000006e+00 -1.999996e+00 -1.000010e+00
#>  [6] -8.504243e-06  1.000003e+00  1.999972e+00  3.000000e+00  3.999998e+00
#> [11]  4.999976e+00