Standardized Generalized Hyperbolic Distribution

Density, distribution function, quantile function and random generation for the standardized generalized hyperbolic distribution.

Usage

dsgh(x, zeta = 1, rho = 0, lambda = 1, log = FALSE)
psgh(q, zeta = 1, rho = 0, lambda = 1)
qsgh(p, zeta = 1, rho = 0, lambda = 1)
rsgh(n, zeta = 1, rho = 0, lambda = 1)

Arguments

x, q

a numeric vector of quantiles.

p

a numeric vector of probabilities.

n

number of observations.

zeta

shape parameter, a positive number.

rho

skewness parameter, a number in the range \((-1, 1)\).

lambda

??

log

a logical flag by default FALSE. If TRUE, log values are returned.

Value

numeric vector

Details

dsgh gives the density, psgh gives the distribution function, qsgh gives the quantile function, and rsgh generates random deviates.

The generator rsgh is based on the GH algorithm given by Scott (2004).

Author

Diethelm Wuertz

Examples

## rsgh -
   set.seed(1953)
   r = rsgh(5000, zeta = 1, rho = 0.5, lambda = 1)
   plot(r, type = "l", col = "steelblue",
     main = "gh: zeta=1 rho=0.5 lambda=1")

 
## dsgh - 
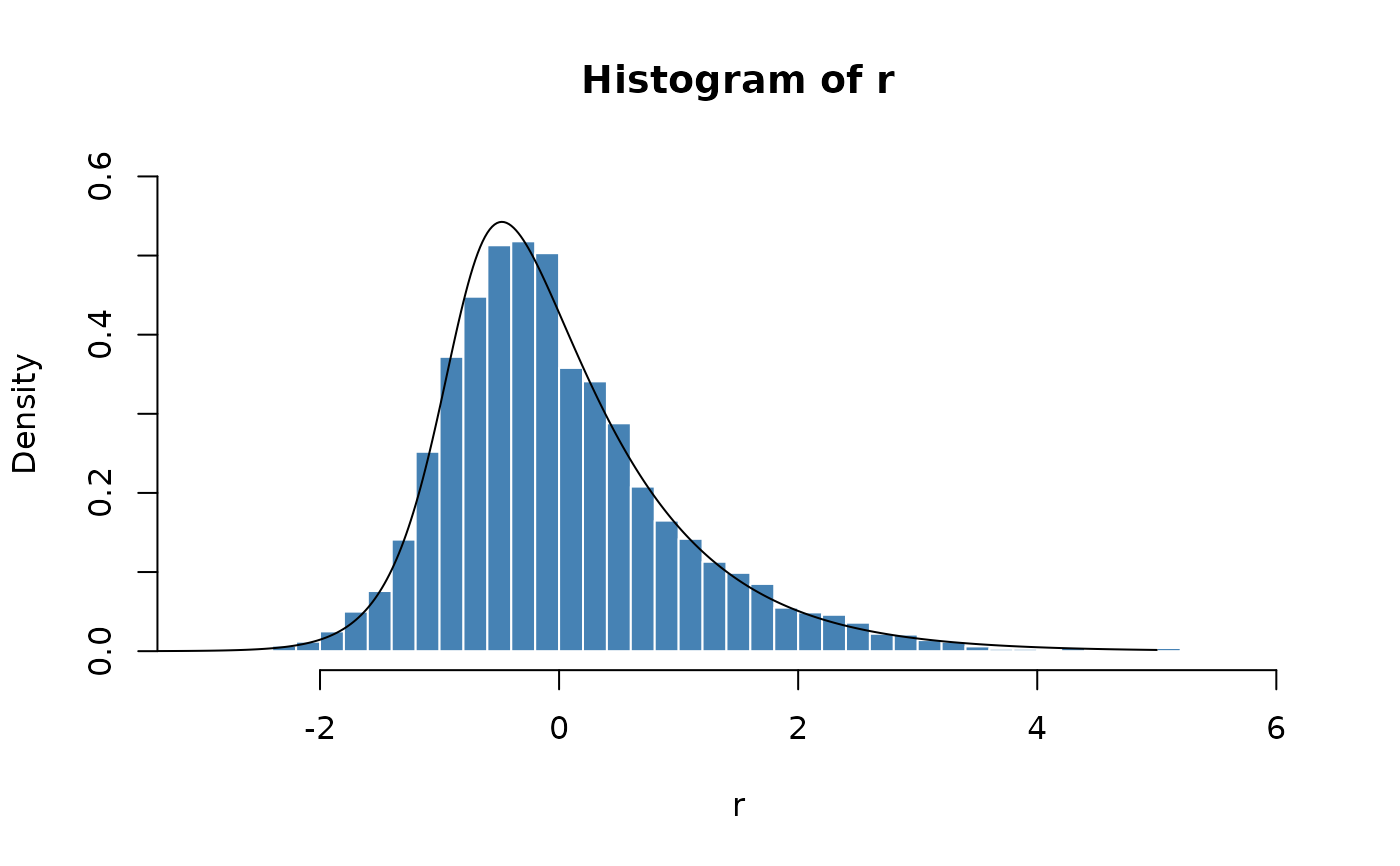
   # Plot empirical density and compare with true density:
   hist(r, n = 50, probability = TRUE, border = "white", col = "steelblue",
     ylim = c(0, 0.6))
   x = seq(-5, 5, length = 501)
   lines(x, dsgh(x, zeta = 1, rho = 0.5, lambda = 1))

 
## psgh -  
   # Plot df and compare with true df:
   plot(sort(r), (1:5000/5000), main = "Probability", col = "steelblue")
   lines(x, psgh(x, zeta = 1, rho = 0.5, lambda = 1))

   
## qsgh -
   # Compute Quantiles:
   round(qsgh(psgh(seq(-5, 5, 1), zeta = 1, rho = 0.5), zeta = 1, rho = 0.5), 4)
#>  [1] -5 -4 -3 -2 -1  0  1  2  3  4  5