Standardized Normal Inverse Gaussian Distribution

Density, distribution function, quantile function and random generation for the standardized normal inverse Gaussian distribution.

Usage

dsnig(x, zeta = 1, rho = 0, log = FALSE)
psnig(q, zeta = 1, rho = 0)
qsnig(p, zeta = 1, rho = 0)
rsnig(n, zeta = 1, rho = 0)

Arguments

x, q

a numeric vector of quantiles.

p

a numeric vector of probabilities.

n

number of observations.

zeta

shape parameter zeta is positive.

rho

skewness parameter, a number in the range \((-1, 1)\).

log

a logical flag by default FALSE. If TRUE, log values are returned.

Details

dsnig gives the density, psnig gives the distribution function, qsnig gives the quantile function, and rsnig generates random deviates.

The random deviates are calculated with the method described by Raible (2000).

Value

numeric vector

Author

Diethelm Wuertz

Examples

## snig -
   set.seed(1953)
   r = rsnig(5000, zeta = 1, rho = 0.5)
   plot(r, type = "l", col = "steelblue",
     main = "snig: zeta=1 rho=0.5")

 
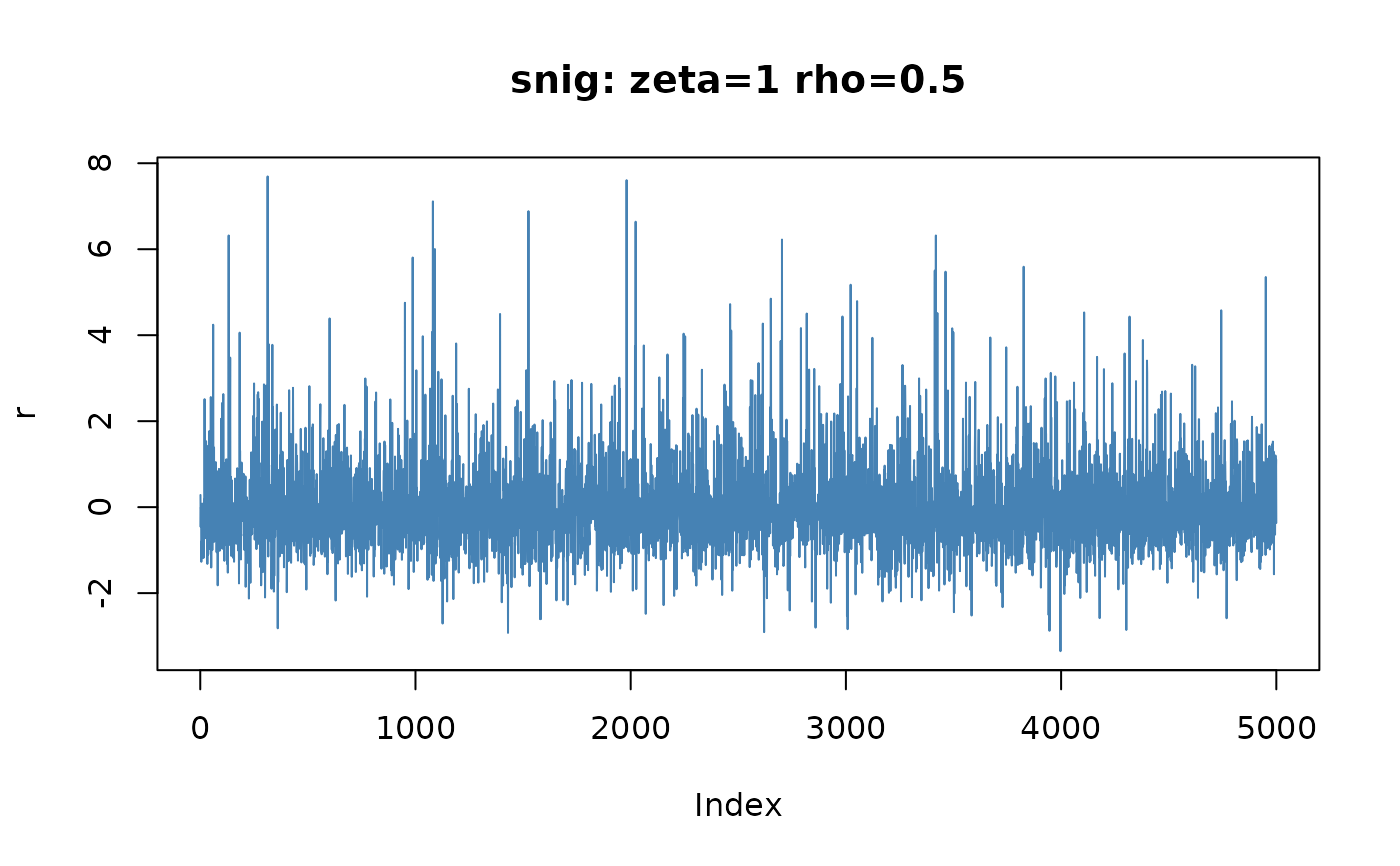## snig - 
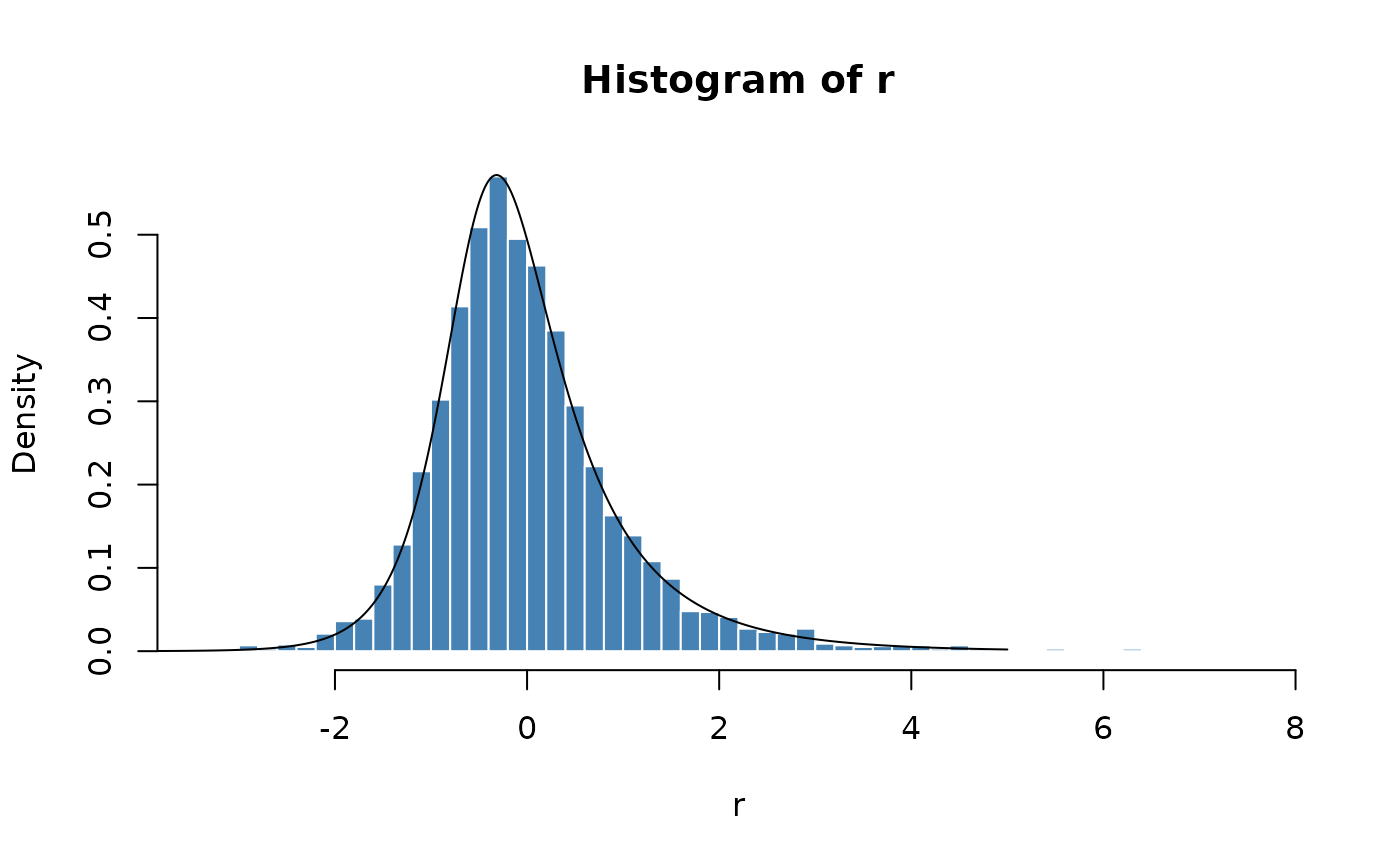
   # Plot empirical density and compare with true density:
   hist(r, n = 50, probability = TRUE, border = "white", col = "steelblue")
   x = seq(-5, 5, length = 501)
   lines(x, dsnig(x, zeta = 1, rho = 0.5))

 
## snig -  
   # Plot df and compare with true df:
   plot(sort(r), (1:5000/5000), main = "Probability", col = "steelblue")
   lines(x, psnig(x, zeta = 1, rho = 0.5))

   
## snig -
   # Compute Quantiles:
   qsnig(psnig(seq(-5, 5, 1), zeta = 1, rho = 0.5), zeta = 1, rho = 0.5) 
#>  [1] -5.000000e+00 -3.999999e+00 -2.999983e+00 -2.000011e+00 -1.000000e+00
#>  [6] -2.609555e-07  1.000004e+00  2.000016e+00  3.000001e+00  4.000000e+00
#> [11]  5.000029e+00