Drawdown statistics

A collection of functions which compute drawdown statistics. Included are density, distribution function, and random generation for the maximum drawdown distribution. In addition the expectation of drawdowns for Brownian motion can be computed.

Usage

dmaxdd(x, sd = 1, horizon = 100, N = 1000) 
pmaxdd(q, sd = 1, horizon = 100, N = 1000) 
rmaxdd(n, mean = 0, sd = 1, horizon = 100)

maxddStats(mean = 0, sd = 1, horizon = 1000)

Arguments

x, q

a numeric vector of quantiles.

n

an integer value, the number of observations.

mean, sd

two numeric values, the mean and standard deviation.

horizon

an integer value, the (run time) horizon of the investor.

N

an integer value, the precession index for summations. Before you change this value please inspect Magdon-Ismail et. al. (2003).

Details

dmaxdd computes the density function of the maximum drawdown distribution. pmaxdd computes the distribution function. rmaxdd generates random numbers from that distribution. maxddStats computes the expectation of drawdowns.

dmaxdd returns for a trendless Brownian process mean=0 and standard deviation "sd" the density from the probability that the maximum drawdown "D" is larger or equal to "h" in the interval [0,T], where "T" denotes the time horizon of the investor.

pmaxdd returns for a trendless Brownian process mean=0 and standard deviation "sd" the probability that the maximum drawdown "D" is larger or equal to "h" in the interval [0,T], where "T" denotes the time horizon of the investor.

rmaxdd returns for a Brownian Motion process with mean mean and standard deviation sd random variates of maximum drawdowns.

maxddStats returns the expected value, E[D], of maximum drawdowns of Brownian Motion for a given drift mean, variance sd, and runtime horizon of the Brownian Motion process.

Note

Currrently, only the driftless case is implemented.

References

Magdon-Ismail M., Atiya A.F., Pratap A., Abu-Mostafa Y.S. (2003); On the Maximum Drawdown of a Brownian Motion, Preprint, CalTech, Pasadena USA, p. 24.

Examples

## rmaxdd
## Set a random seed
set.seed(1953)               
## horizon of the investor, time T
horizon <- 1000               
## number of MC samples, N -> infinity
samples <- 1000               
## Range of expected Drawdons
xlim <- c(0, 5) * sqrt(horizon) 

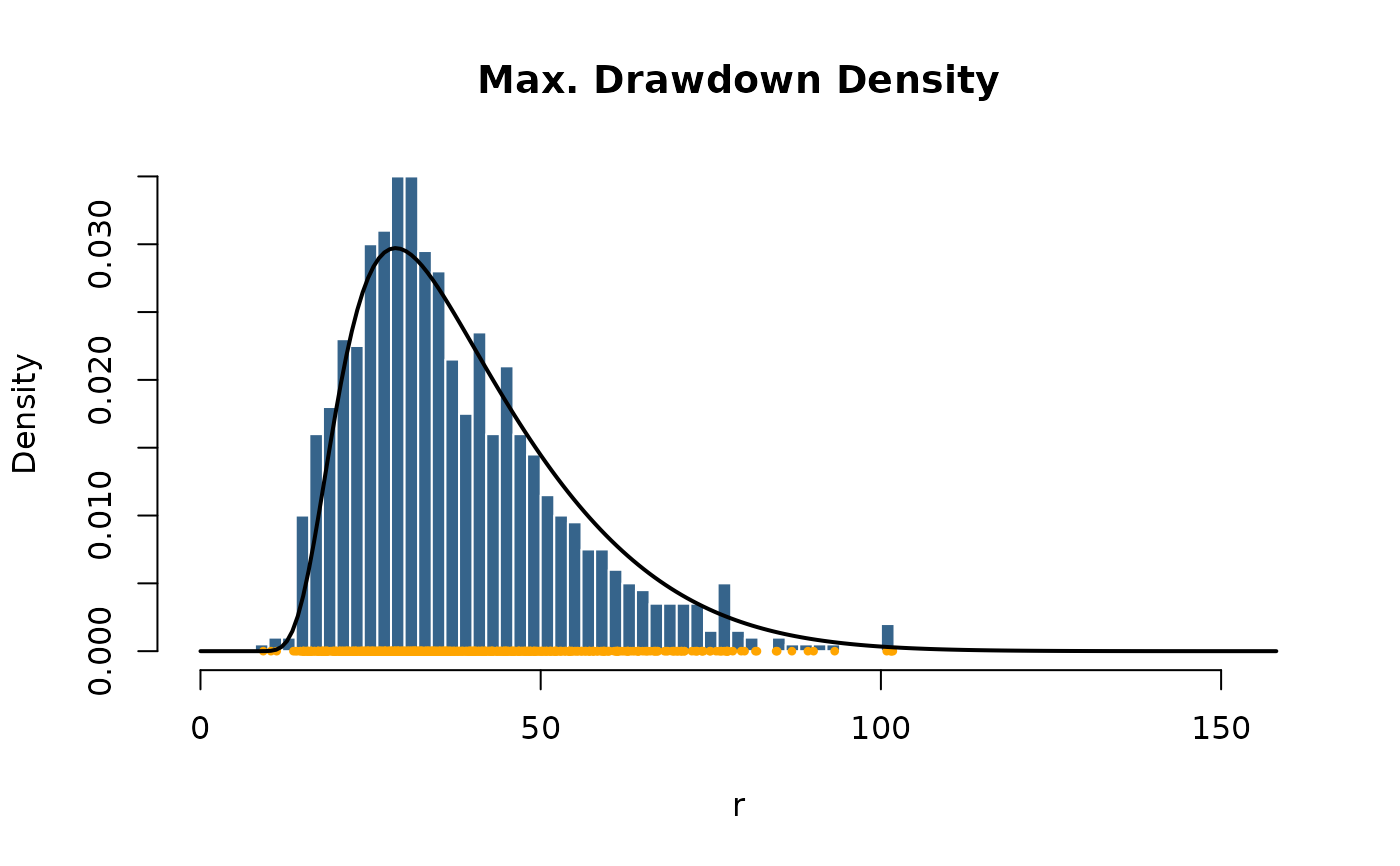
## Plot Histogram of Simulated Max Drawdowns:
r <- rmaxdd(n = samples, mean = 0, sd = 1, horizon = horizon)
hist(x = r, n = 40, probability = TRUE, xlim = xlim, 
     col = "steelblue4", border = "white", main = "Max. Drawdown Density") 
points(r, rep(0, samples), pch = 20, col = "orange", cex = 0.7)
   
## dmaxdd
x <- seq(0, xlim[2], length = 200)
d <- dmaxdd(x = x, sd = 1, horizon = horizon, N = 1000)
lines(x, d, lwd = 2)

    
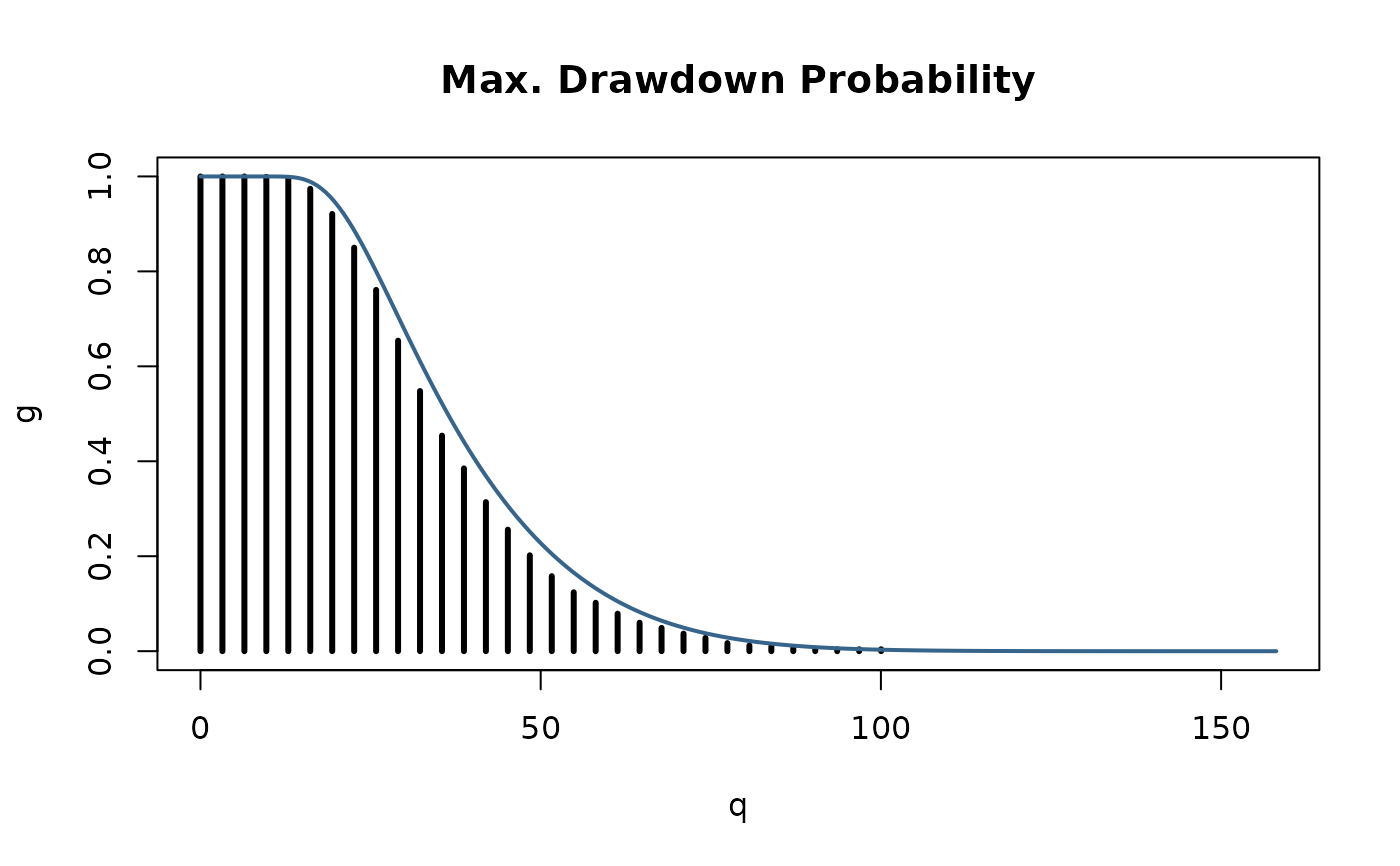
## pmaxdd
## Count Frequencies of Drawdowns Greater or Equal to "h":
n <- 50
x <- seq(0, xlim[2], length = n)
g <- rep(0, times = n)
for (i in 1:n)
    g[i] <- length (r[r > x[i]]) / samples

plot(x, g, type ="h", lwd = 3,
     xlab = "q", main = "Max. Drawdown Probability")
## Compare with True Probability "G_D(h)":
x <- seq(0, xlim[2], length = 5*n)
p <- pmaxdd(q = x, sd = 1, horizon = horizon, N = 5000)
lines(x, p, lwd = 2, col="steelblue4") 

   
## maxddStats
## Compute expectation Value E[D]:
maxddStats(mean = -0.5, sd = 1, horizon = 10^(1:4))
#> [1]    6.841696   52.000000  502.000000 5002.000000
maxddStats(mean =  0.0, sd = 1, horizon = 10^(1:4))
#> [1]   3.963327  12.533141  39.633273 125.331414
maxddStats(mean =  0.5, sd = 1, horizon = 10^(1:4))
#> [1] 2.529253 4.566413 6.809237 9.101853