GH Distribution Fit

Estimates the distrinbutional parameters for a generalized hyperbolic distribution.

Usage

ghFit(x, alpha = 1, beta = 0, delta = 1, mu = 0, lambda = -1/2, 
    scale = TRUE, doplot = TRUE, span = "auto", trace = TRUE, 
    title = NULL, description = NULL, ...)

Arguments

x

a numeric vector.

alpha

first shape parameter.

beta

second shape parameter, should in the range (0, alpha).

delta

scale parameter, must be zero or positive.

mu

location parameter, by default 0.

lambda

defines the sublclass, by default \(-1/2\).

scale

a logical flag, by default TRUE. Should the time series be scaled by its standard deviation to achieve a more stable optimization?

doplot

a logical flag. Should a plot be displayed?

span

x-coordinates for the plot, by default 100 values automatically selected and ranging between the 0.001, and 0.999 quantiles. Alternatively, you can specify the range by an expression like span=seq(min, max, times = n), where, min and max are the left and right endpoints of the range, and n gives the number of the intermediate points.

trace

a logical flag. Should the parameter estimation process be traced?

title

a character string which allows for a project title.

description

a character string which allows for a brief description.

...

parameters to be parsed.

Value

an object from class "fDISTFIT". Slot fit is a list, currently with components estimate, minimum and code.

Details

The meanings of the parameters correspond to the first parameterization, see gh for further details.

The function nlm is used to minimize the "negative" maximum log-likelihood function. nlm carries out a minimization using a Newton-type algorithm.

Examples

set.seed(1953)
s <- rgh(n = 1000, alpha = 1.5, beta = 0.3, delta = 0.5, mu = -1.0) 

ghFit(s, alpha = 1, beta = 0, delta = 1, mu = mean(s), doplot = TRUE, trace = FALSE) 

#> 
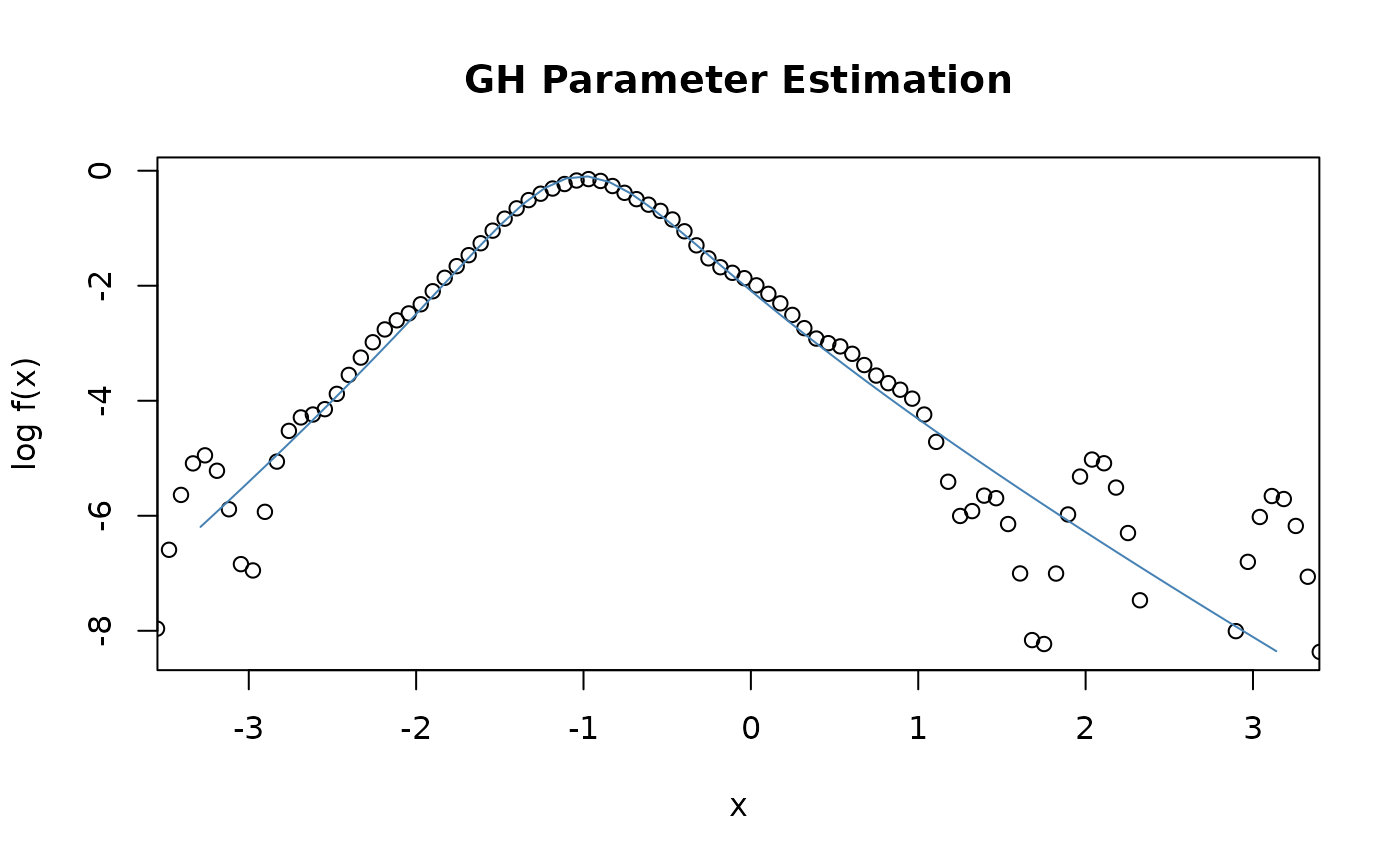#> Title:
#>  Generalized Hyperbolic Parameter Estimation 
#> 
#> Call:
#>  ghFit(x = s, alpha = 1, beta = 0, delta = 1, mu = mean(s), doplot = TRUE, 
#>     trace = FALSE)
#> 
#> Model:
#>  Generalized Hyperbolic Distribution
#> 
#> Estimated Parameter(s):
#>      alpha       beta      delta         mu     lambda 
#>  1.7443507  0.3284269  0.5633309 -1.0458067 -0.4132735 
#>