Skip to contents

Bivariate Krige Interpolation

stats-interpKrige.Rd

Bivariate Krige Interpolation.

Usage

krigeInterp(x, y = NULL, z = NULL, gridPoints = 21,
    xo = seq(min(x), max(x), length = gridPoints),
    yo = seq(min(y), max(y), length = gridPoints),
    extrap = FALSE, polDegree = 6)

Arguments

x, y, z

the arguments x and y are two numeric vectors of grid pounts, and z is a numeric matrix or any other rectangular object which can be transformed by the function as.matrix into a matrix object.

gridPoints

an integer value specifying the number of grid points in x and y direction.

xo, yo

two numeric vectors of data points spanning the grid.

extrap

a logical, if TRUE then the data points are extrapolated.

polDegree

the polynomial krige degree, an integer ranging between 1 and 6.

Note

krigeInterp() requires package spatial.

Value

a list with at least three entries, x, y and z. The returned values can be used directly in persp and contour 3D plotting methods.

See also

akimaInterp, linearInterp.

Examples

# \donttest{
## The akima library is not auto-installed because of a different licence.
## krigeInterp -  Kriging:
set.seed(1953)
x = runif(999) - 0.5
y = runif(999) - 0.5
z = cos(2*pi*(x^2+y^2))
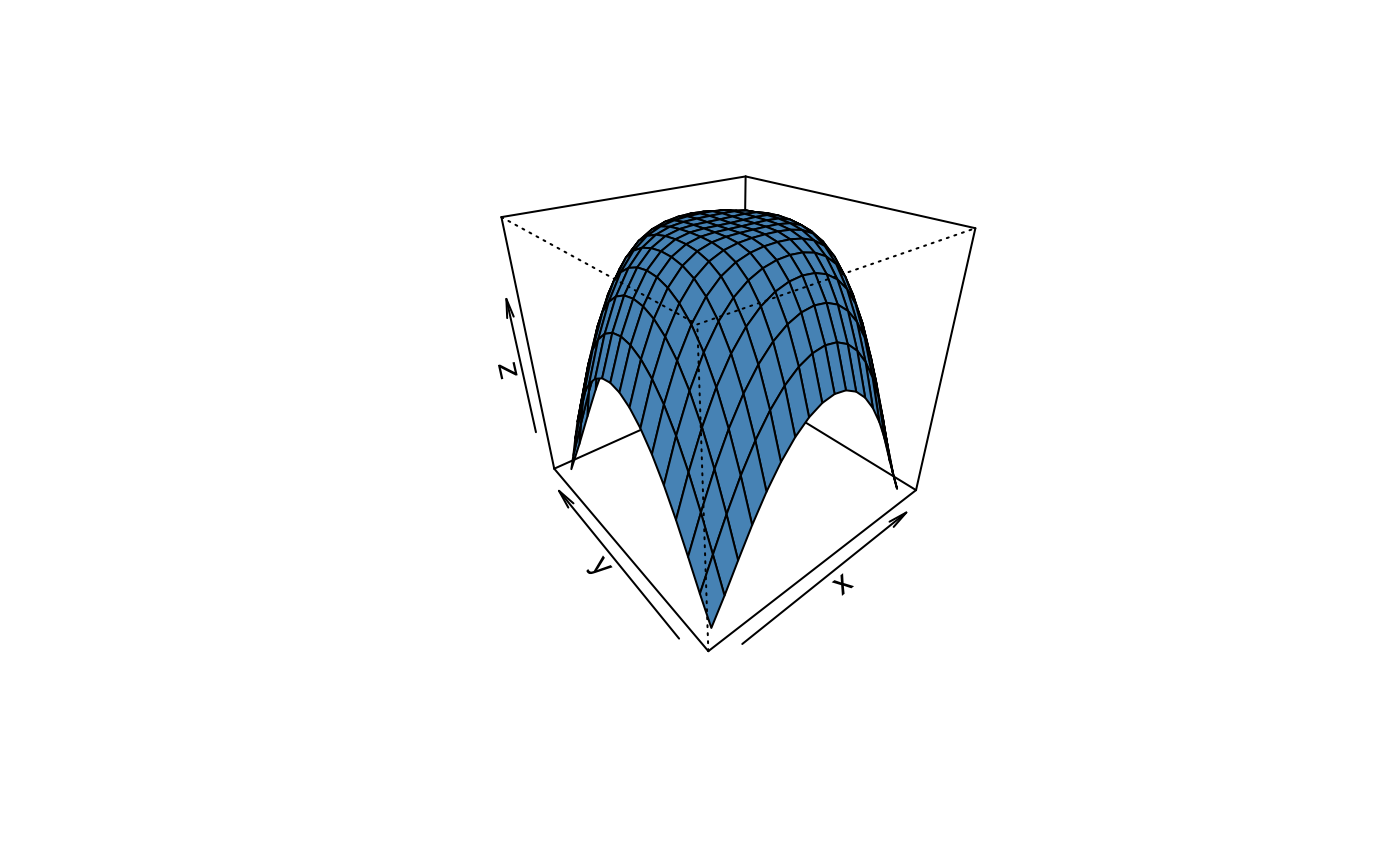
ans = krigeInterp(x, y, z, extrap = FALSE)
persp(ans, theta = -40, phi = 30, col = "steelblue",
    xlab = "x", ylab = "y", zlab = "z")

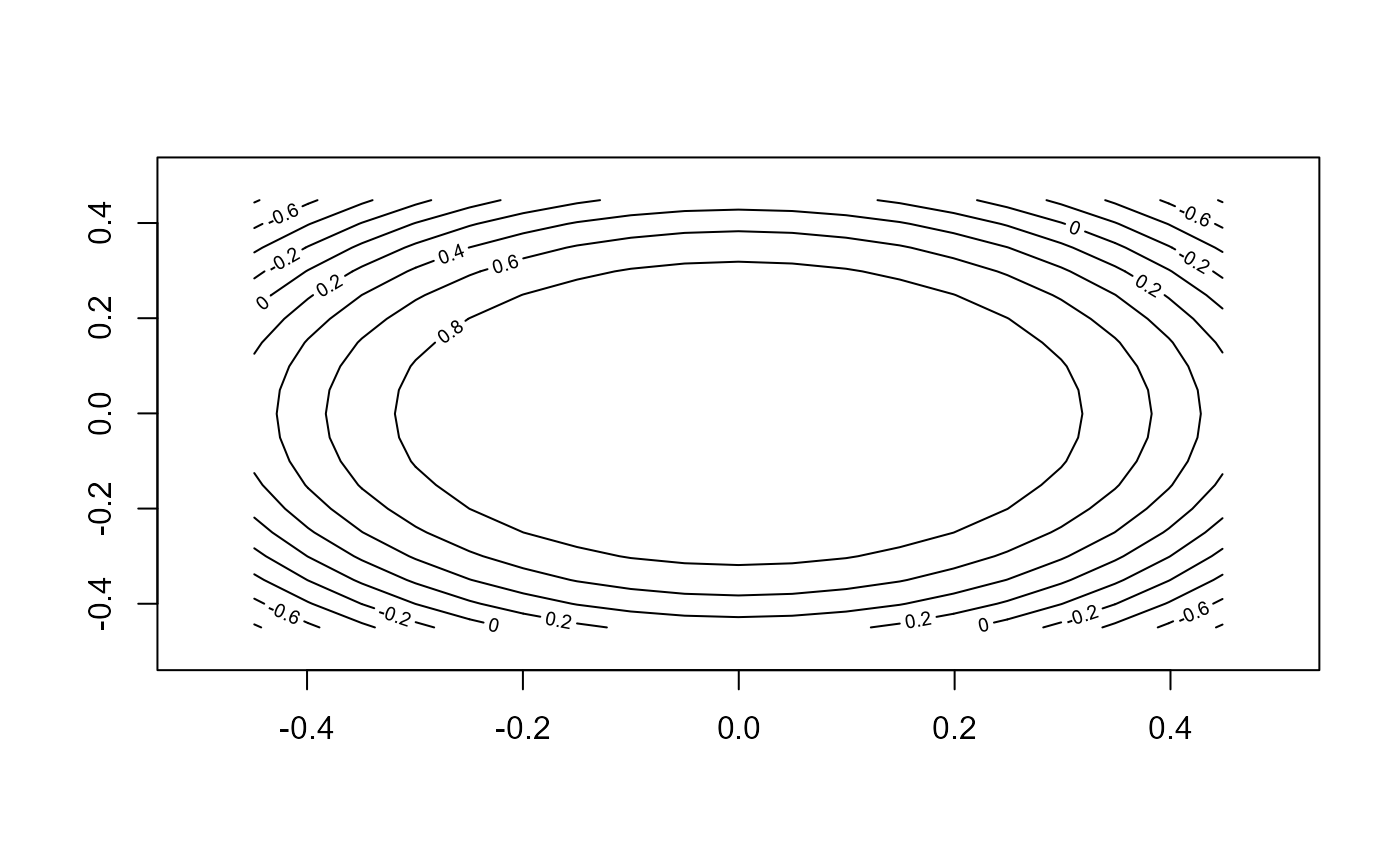
contour(ans)

# }