Conditional moments of MixAR models
mix_moment.RdConditional moments of MixAR models.
Usage
mix_location(model, x, index, xcond)
mix_variance(model, x, index, xcond)
mix_central_moment(model, x, index, xcond, k)
mix_moment(model, x, index, xcond, k)
mix_kurtosis(...)
mix_ekurtosis(...)Arguments
- model
a MixAR object.
- x
a time series.
- index
a vector of indices in
xfor which to compute the requested property. If missing, the computation is done for all indices greater thanmax(model@order).- xcond
a time series, the point prediction is computed for the first value after the end of the time series. Only the last
max(model@order)values inxcondare used.- k
a positive integer specifying the moment to compute.
- ...
passed on to
mix_central_moment.
Details
These functions compute conditional moments and related quantities.
kurtosis and ekurtosis compute conditional kurtosis and
excess kurtosis, respectively. Effectively, they have the same
parameters as mix_central_moment, since they pass "..."
to it along with k = 4. It is an error to supply argument
k to the kurtosis functions.
Value
when called with one argument (model), a function with argument xcond;
otherwise if xcond is not missing, a single numeric value;
otherwise a vector of length length(index).
References
Boshnakov GN (2009). “Analytic expressions for predictive distributions in mixture autoregressive models.” Stat. Probab. Lett., 79(15), 1704-1709. doi:10.1016/j.spl.2009.04.009 .
Note
I wrote the above description recently from reading six years old code, it may need further verification.
Examples
## data(ibmclose, package = "fma") # `ibmclose'
ibmclose <- as.numeric(fma::ibmclose)
length(ibmclose) # 369
#> [1] 369
max(exampleModels$WL_ibm@order) # 2
#> [1] 2
## compute point predictions for t = 3,...,369
pred <- mix_location(exampleModels$WL_ibm, ibmclose)
plot(pred)
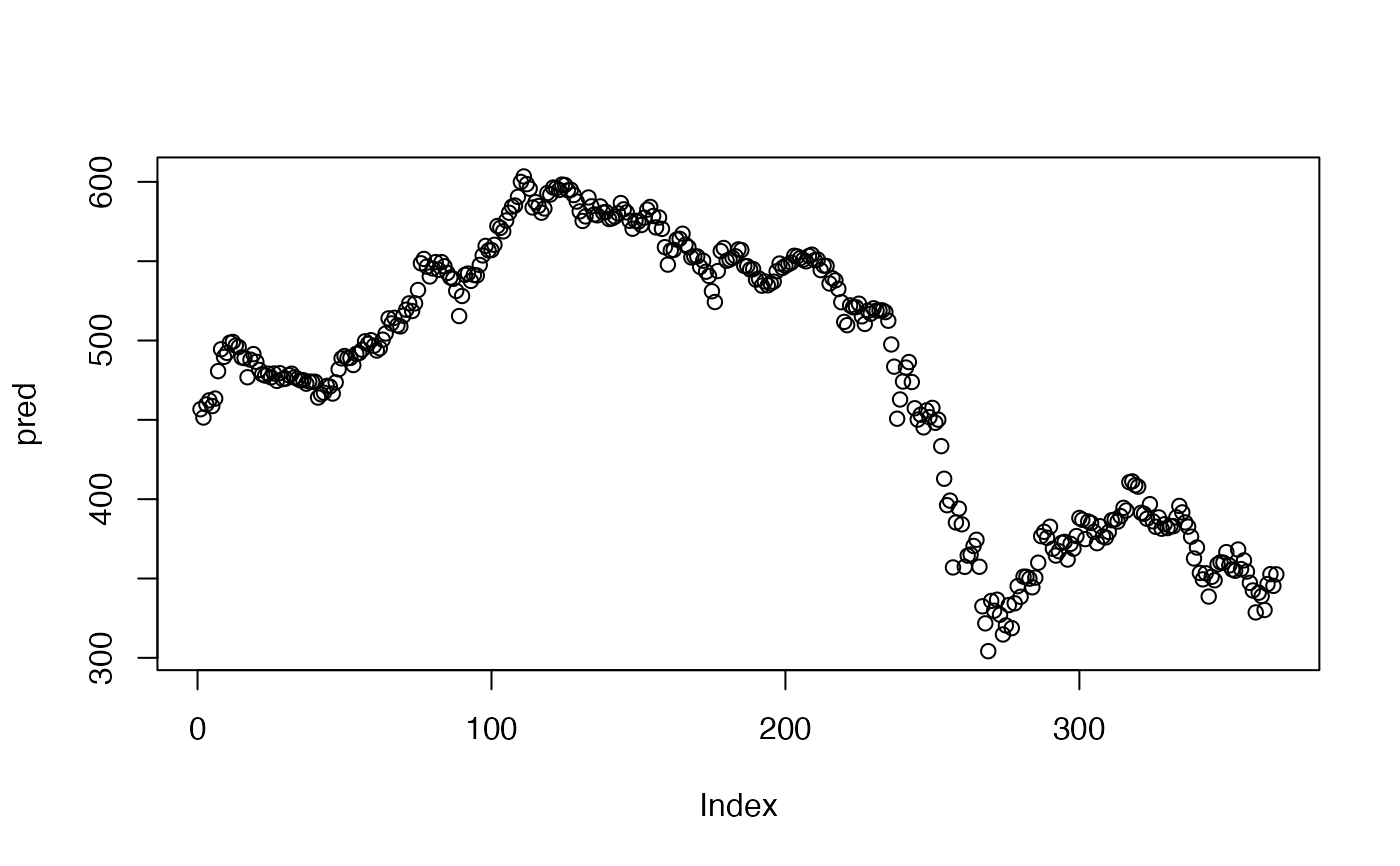 ## compute one-step point predictions for t = 360,...369
mix_location(exampleModels$WL_ibm, ibmclose, index = 369 - 9:0 )
#> [1] 347.2596 342.4712 328.6250 341.0577 338.8942 330.1539 346.4808 352.7404
#> [9] 345.3654 352.6346
f <- mix_location(exampleModels$WL_ibm) # a function
## predict the value after the last
f(ibmclose)
#> [1] 357.5288
## a different way to compute one-step point predictions for t = 360,...369
sapply(369 - 10:1, function(k) f(ibmclose[1:k]))
#> [1] 347.2596 342.4712 328.6250 341.0577 338.8942 330.1539 346.4808 352.7404
#> [9] 345.3654 352.6346
## the results are the same, but notice that xcond gives past values
## while index above specifies the times for which to compute the predictions.
identical(sapply(369 - 10:1, function(k) f(ibmclose[1:k])),
mix_location(exampleModels$WL_ibm, ibmclose, index = 369 - 9:0 ))
#> [1] TRUE
## conditional variance
f <- mix_variance(exampleModels$WL_ibm) # a function
## predict the value after the last
f(ibmclose)
#> [1] 5.821599
## a different way to compute one-step point predictions for t = 360,...369
sapply(369 - 10:1, function(k) f(ibmclose[1:k]))
#> [1] 11.410334 5.821599 39.354008 23.286395 0.232864 14.903293 45.641335
#> [8] 11.410334 8.383102 8.383102
## the results are the same, but notice that xcond gives past values
## while index above specifies the times for which to compute the predictions.
identical(sapply(369 - 10:1, function(k) f(ibmclose[1:k])),
mix_variance(exampleModels$WL_ibm, ibmclose, index = 369 - 9:0 ))
#> [1] TRUE
# interesting example
# bimodal distribution, low kurtosis, 4th moment not much larger than 2nd
moWL <- exampleModels$WL_ibm
mix_location(moWL,xcond = c(500,450))
#> [1] 444.7116
mix_kurtosis(moWL,xcond = c(500,450))
#> [1] 1.298194
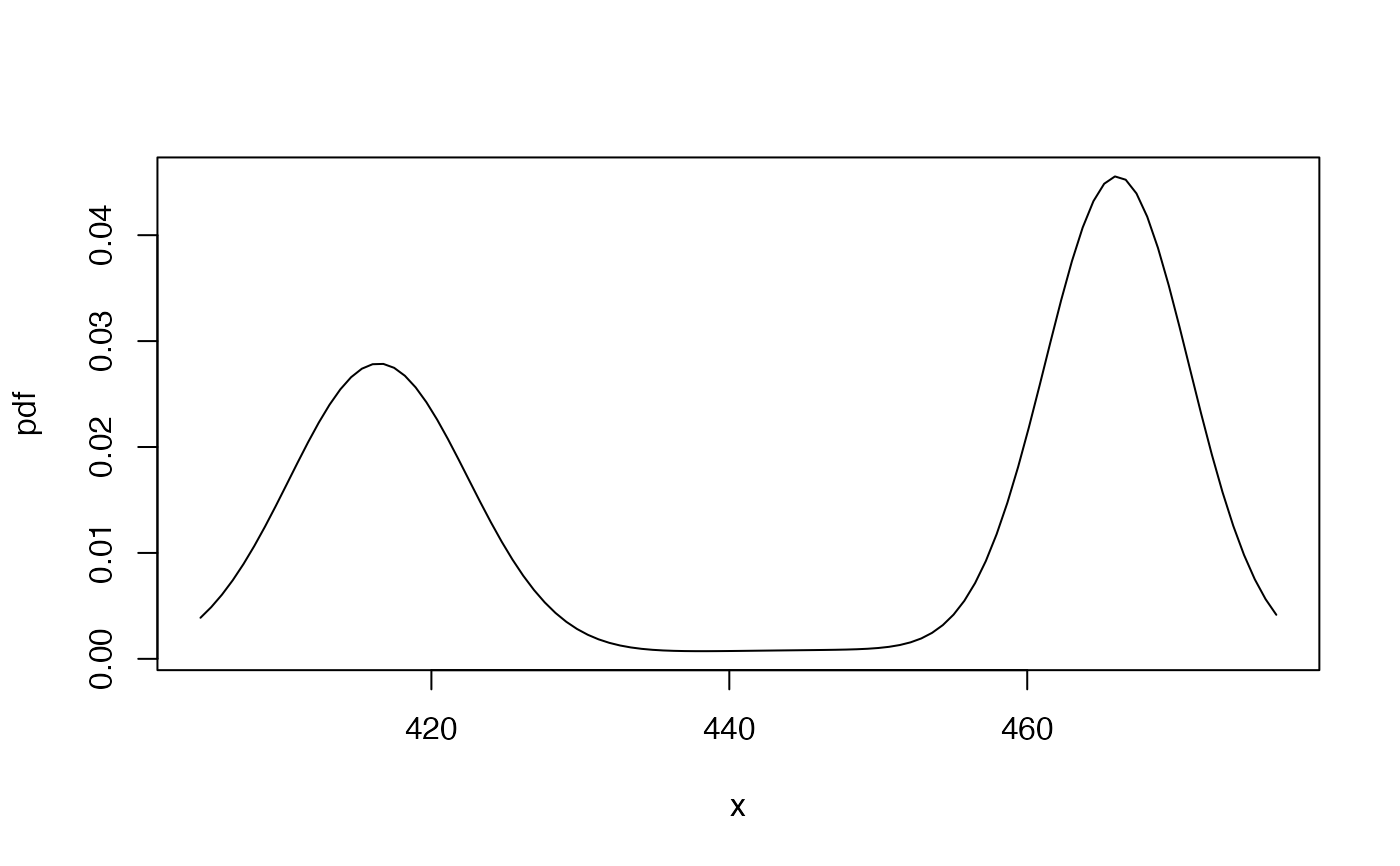
f1pdf <- mix_pdf(moWL,xcond = c(500,450))
f1cdf <- mix_cdf(moWL,xcond = c(500,450))
gbutils::plotpdf(f1pdf,cdf=f1cdf)
## compute one-step point predictions for t = 360,...369
mix_location(exampleModels$WL_ibm, ibmclose, index = 369 - 9:0 )
#> [1] 347.2596 342.4712 328.6250 341.0577 338.8942 330.1539 346.4808 352.7404
#> [9] 345.3654 352.6346
f <- mix_location(exampleModels$WL_ibm) # a function
## predict the value after the last
f(ibmclose)
#> [1] 357.5288
## a different way to compute one-step point predictions for t = 360,...369
sapply(369 - 10:1, function(k) f(ibmclose[1:k]))
#> [1] 347.2596 342.4712 328.6250 341.0577 338.8942 330.1539 346.4808 352.7404
#> [9] 345.3654 352.6346
## the results are the same, but notice that xcond gives past values
## while index above specifies the times for which to compute the predictions.
identical(sapply(369 - 10:1, function(k) f(ibmclose[1:k])),
mix_location(exampleModels$WL_ibm, ibmclose, index = 369 - 9:0 ))
#> [1] TRUE
## conditional variance
f <- mix_variance(exampleModels$WL_ibm) # a function
## predict the value after the last
f(ibmclose)
#> [1] 5.821599
## a different way to compute one-step point predictions for t = 360,...369
sapply(369 - 10:1, function(k) f(ibmclose[1:k]))
#> [1] 11.410334 5.821599 39.354008 23.286395 0.232864 14.903293 45.641335
#> [8] 11.410334 8.383102 8.383102
## the results are the same, but notice that xcond gives past values
## while index above specifies the times for which to compute the predictions.
identical(sapply(369 - 10:1, function(k) f(ibmclose[1:k])),
mix_variance(exampleModels$WL_ibm, ibmclose, index = 369 - 9:0 ))
#> [1] TRUE
# interesting example
# bimodal distribution, low kurtosis, 4th moment not much larger than 2nd
moWL <- exampleModels$WL_ibm
mix_location(moWL,xcond = c(500,450))
#> [1] 444.7116
mix_kurtosis(moWL,xcond = c(500,450))
#> [1] 1.298194
f1pdf <- mix_pdf(moWL,xcond = c(500,450))
f1cdf <- mix_cdf(moWL,xcond = c(500,450))
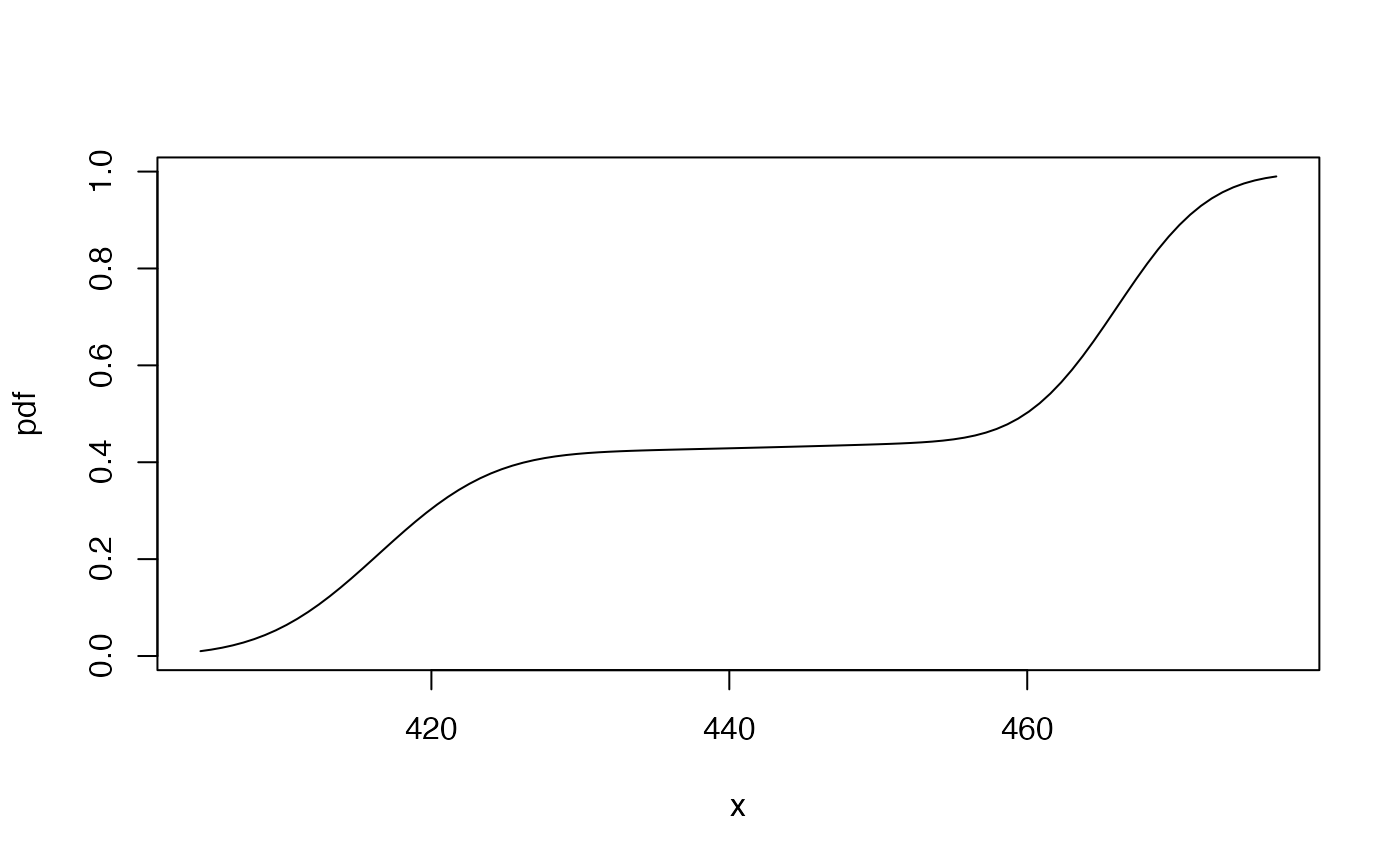
gbutils::plotpdf(f1pdf,cdf=f1cdf)
 gbutils::plotpdf(f1cdf,cdf=f1cdf)
gbutils::plotpdf(f1cdf,cdf=f1cdf)
 f1cdf(c(400,480))
#> [1] 0.001408424 0.997066707
mix_variance(moWL,xcond = c(500,450))
#> [1] 622.5978
mix_central_moment(moWL,xcond = c(500,450), k=2)
#> [1] 622.5978
sqrt(mix_variance(moWL,xcond = c(500,450)))
#> [1] 24.95191
sqrt(mix_central_moment(moWL,xcond = c(500,450), k=2))
#> [1] 24.95191
f1cdf(c(400,480))
#> [1] 0.001408424 0.997066707
mix_variance(moWL,xcond = c(500,450))
#> [1] 622.5978
mix_central_moment(moWL,xcond = c(500,450), k=2)
#> [1] 622.5978
sqrt(mix_variance(moWL,xcond = c(500,450)))
#> [1] 24.95191
sqrt(mix_central_moment(moWL,xcond = c(500,450), k=2))
#> [1] 24.95191