Prepare SARIMA simulations

Prepare SARIMA simulations.

Usage

prepareSimSarima(model, x = NULL, eps = NULL, n, n.start = NA,
                 xintercept = NULL, rand.gen = rnorm)

# S3 method for simSarimaFun
print(x, ...)

Arguments

model

an object from a suitable class or a list, see Details.

x

initial/before values of the time series, a list, a numeric vector or time series, see Details.

eps

initial/before values of the innovations, a list or a numeric vector, see Details.

n

number of observations to generate, if missing an attempt is made to infer it from x and eps.

n.start

number of burn-in observations.

xintercept

non-constant intercept which may represent trend or covariate effects.

rand.gen

random number generator, defaults to N(0,1).

...

ignored.

Details

prepareSimSarima does the preparatory work for simulation from a Sarima model, given the specifications and returns a function, which can be called as many times as needed.

The variance of the innovations is specified by the model and the simulated innovations are multiplied by the corresponding standard deviation. So, it is expected that the random number generator simulates from a standardised distribution.

Argument model can be from any class representing models in the SARIMA family, such as "SarimaModel", or a list with components suitable to be passed to =new()= for such models.

The canonical form of argument x is a list with components before, init and main. If any of these components is missing or NULL, it is filled suitably. Any other components of x are ignored. If x is not a list, it is put in component main. Conceptually, the three components are concatenated in the given order, the simulated values are put in main (before and init are not changed), the before part is dropped and the rest is returned. In effect, before and init can be viewed as initial values but init is considered part of the generated series.

The format for eps is the same as that of x. The lengths of missing components in x are inferred from the corresponding components of eps, and vice versa.

The format for xintercept is the same as that of x and eps.

print.simSarimaFun is a print method for the objects generated by prepareSimSarima.

Value

for prepareSimSarima, a function to simulate time series, see Details. it is typically called multiple times without arguments. All arguments have defaults set by prepareSimSarima.

n: length of the simulated time series,
rand.gen: random number generator,
...: arguments for the random number generator, passed on to arima.sim.

Author

Georgi N. Boshnakov

Examples

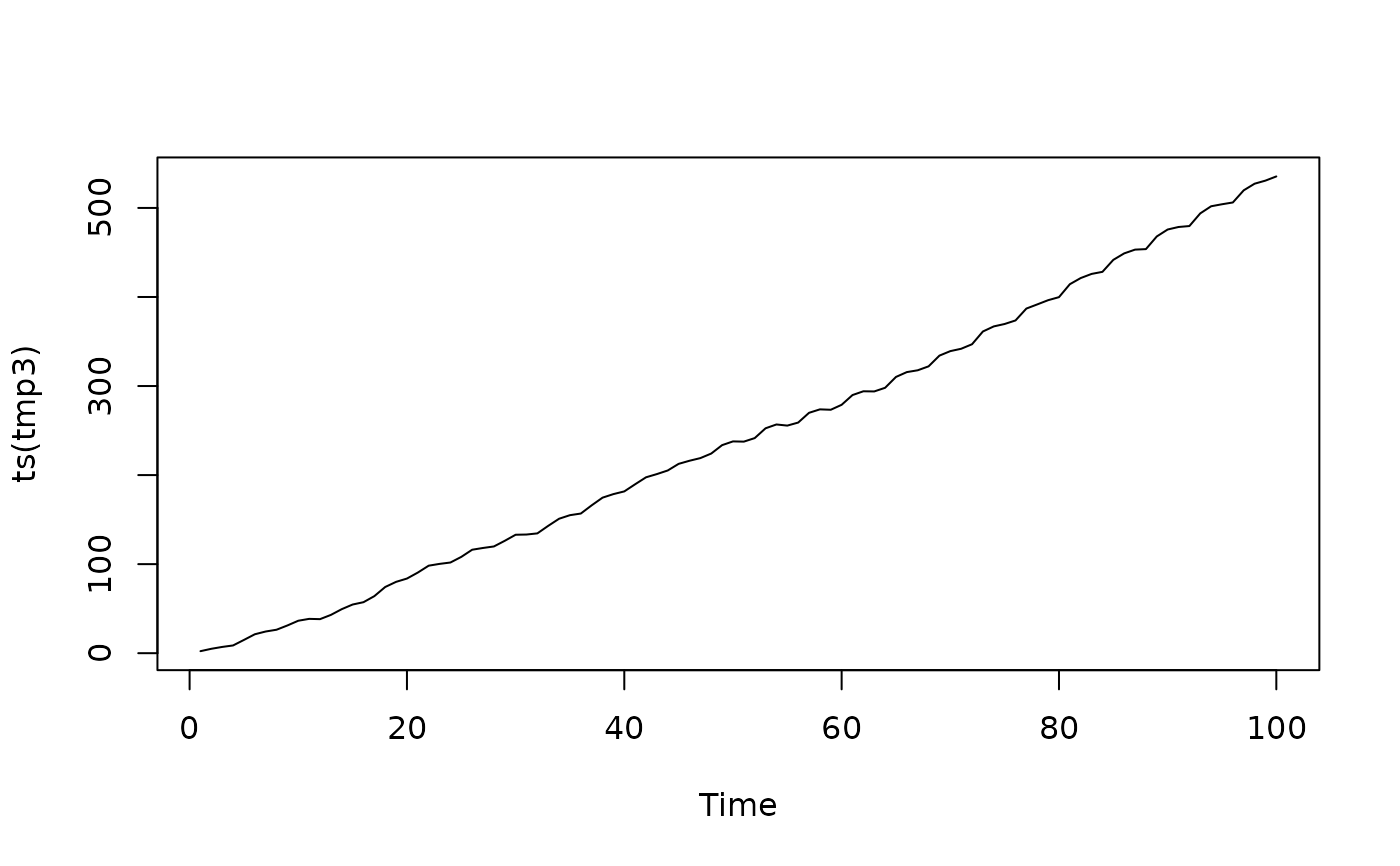
mo1 <- list(ar = 0.9, iorder = 1, siorder = 1, nseasons = 4, sigma2 = 2)
fs1 <- prepareSimSarima(mo1, x = list(before = rep(0,6)),  n = 100)
tmp1 <- fs1()
tmp1
#>   [1]    4.000695    8.148254   11.931620   15.471456   20.004553   23.448029
#>   [7]   24.347732   26.253385   29.371441   29.941756   30.436985   33.363669
#>  [13]   38.078999   40.992003   41.993131   44.850613   50.134660   52.006500
#>  [19]   55.904676   63.243979   74.153931   81.165543   87.685195   98.961783
#>  [25]  115.433202  127.899568  138.626662  154.538047  175.850308  191.557155
#>  [31]  204.338144  222.408688  247.067724  268.983388  285.775668  306.646990
#>  [37]  335.739735  361.798287  383.214974  407.003968  438.251845  466.709624
#>  [43]  488.958496  515.212112  546.883767  576.911106  600.806116  626.681618
#>  [49]  660.425674  692.569202  717.812462  745.719237  781.020246  814.165907
#>  [55]  839.344385  868.013375  902.487260  935.096568  959.542346  987.068564
#>  [61] 1021.472125 1054.613291 1079.181617 1107.560857 1140.394797 1170.761884
#>  [67] 1192.953780 1221.342489 1252.542812 1279.162846 1298.104434 1323.583115
#>  [73] 1350.158073 1372.615300 1387.415328 1409.411949 1431.338943 1448.788218
#>  [79] 1458.122156 1476.819967 1495.050607 1508.649832 1511.918802 1525.219544
#>  [85] 1537.710868 1547.394119 1548.545615 1559.401198 1567.573950 1572.868786
#>  [91] 1570.066187 1576.044438 1578.880902 1580.033961 1575.545291 1578.212966
#>  [97] 1577.288130 1571.870694 1562.584598 1561.826681
plot(ts(tmp1))


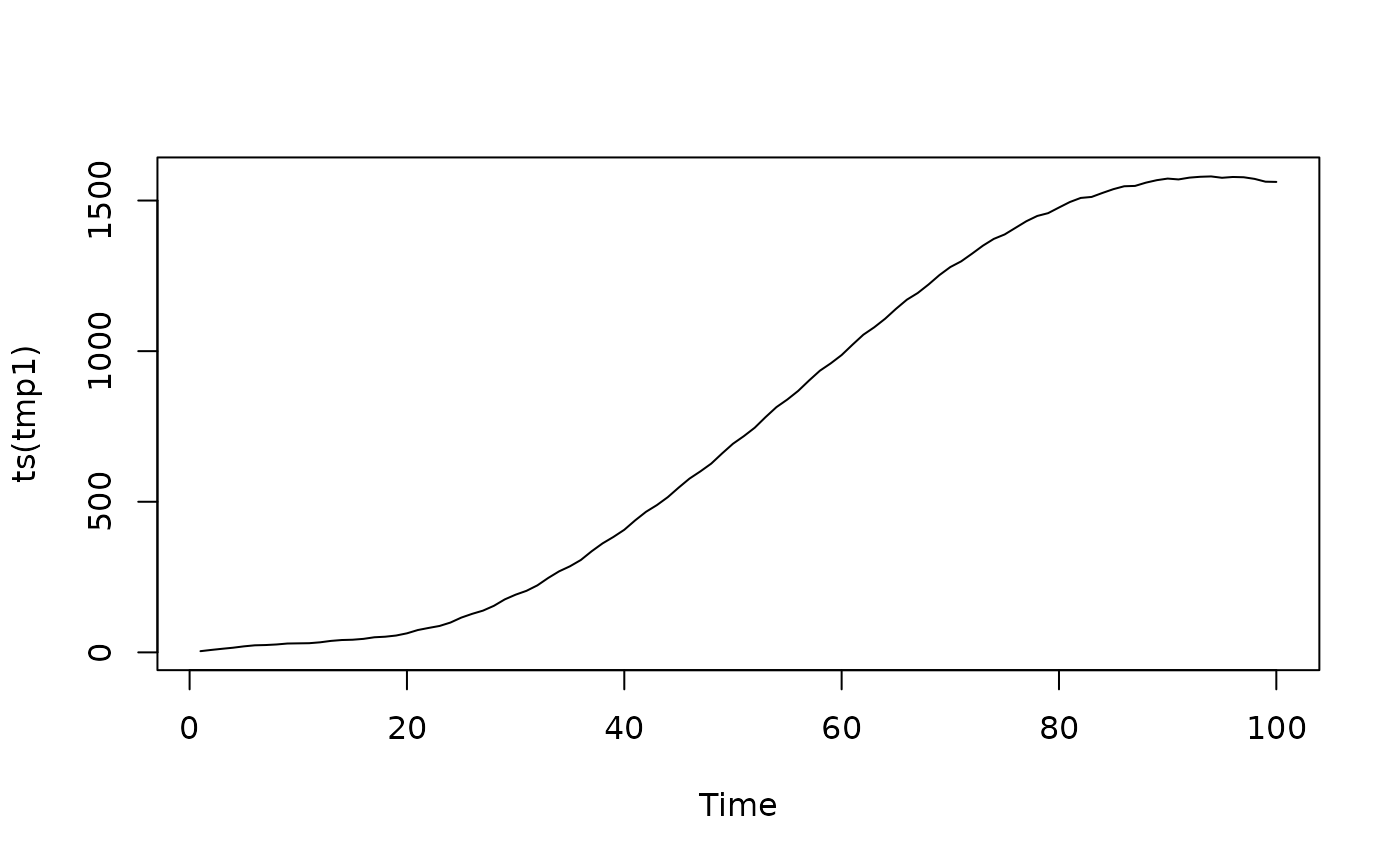fs2 <- prepareSimSarima(mo1, x = list(before = rep(1,6)),  n = 100)
tmp2 <- fs2()
plot(ts(tmp2))


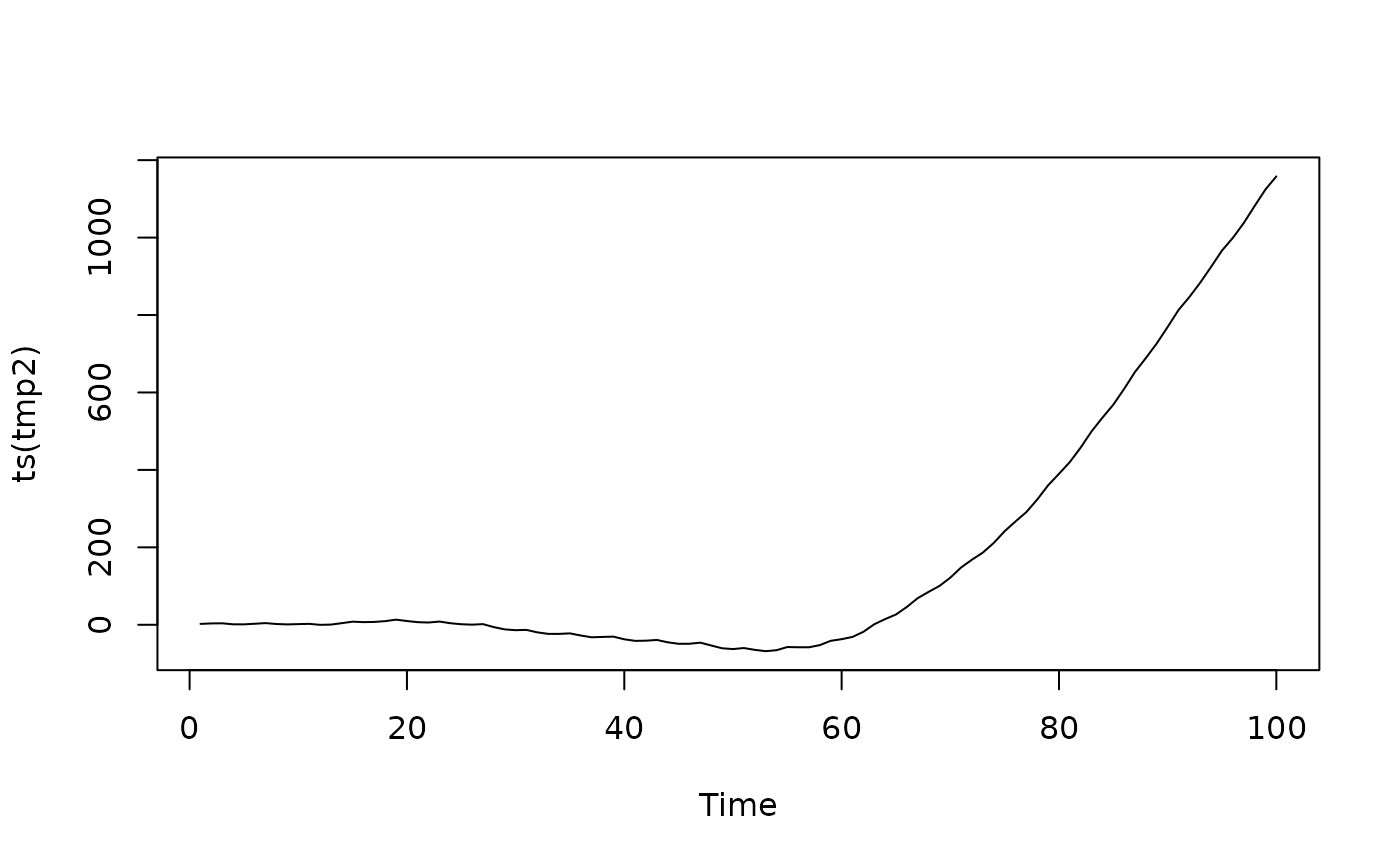mo3 <- mo1
mo3[["ar"]] <- 0.5
fs3 <- prepareSimSarima(mo3, x = list(before = rep(0,6)),  n = 100)
tmp3 <- fs3()
plot(ts(tmp3))