Adjacency graph of classes in packages

Get inheritance graph of classes in one or more packages.

Usage

adjacencyOfClasses(packages, externalSubclasses = FALSE, 
                   result = c("default", "matrixOfPairs", "adjacencyMatrix"), 
                   Wolfram = FALSE)

Arguments

packages: names of one or more packages, a character vector
externalSubclasses: if TRUE, exclude subtrees of classes not defined in any of the packages listed in argument packages.
result: format of the result, can be missing or one of "default", "matrixOfPairs", "adjacencyMatrix", see Details.
Wolfram: if TRUE, print a suitable graph expression to be run by Mathematica, see Details.

Details

adjacencyOfClasses computes a graph representation of the dependencies of S4 classes defined in one or more packages (as specified by argument package) and returns a list. The contents of the list returned by adjacencyOfClasses depend on argument result. Partial matching is used for the value of argument result, e.g., "adj" is equivalent to "adjacencyMatrix".

If externalSubclasses = FALSE, the default, subclasses defined outside the requested packages are excluded. This is typically what the user will be looking for. To get a complete tree, set externalSubclasses to TRUE.

The S4 classes are represented by the vertices of the graph. Component "vertices" of the result gives them as a character vector. References below to the \(i\)th class or vertex correspond to the order in this vector. No attempt is made to arrange the vertices in a particular order. An empty list is returned if this vector is empty.

If result is missing or "default", the edges of the graph are represented by a character vector. Each edge is represented by a string with an arrow "->" from a superclass to a subclass. Here is an example that shows that this package defines one class, which is a subclass of "list":

adjacencyOfClasses("gbutils")
##: $vertices
##: [1] "objectPad" "list"     ##: $edges
##: [1] "list -> objectPad"

This illustrates the effect of argument "externalSubclasses":

adjacencyOfClasses("gbutils", externalSubclasses = TRUE)
##: $vertices
##: [1] "objectPad" "list"      "vector"   ##: $edges
##: [1] "list -> objectPad" "vector -> list"

The edge, "vector -> list" was omitted in the previous example since this relationship is defined elsewhere. This resulted in class "vector" being dropped also from the vertices, since it is not defined in "gbutils" and none of the remaining edges contains it.

If result is "matrixOfPairs", the edges of the graph are represented by a character matrix with two columns, where each row represents an edge from the element in the first column to the element in the second. In this example there is one edge, so the matrix contains one row:

adjacencyOfClasses("gbutils", result = "matrixOfPairs")
##: $vertices
##: [1] "objectPad" "list"     ##: $edges
##:      [,1]   [,2]       
##: [1,] "list" "objectPad"

If result is "adjacencyMatrix", the adjacency matrix of the graph is in component "AM" of the returned list. Element \((i,j)\) of this matrix is equal to one, if the \(j\)th class is a superclass to the \(i\)th. In other words, the \(j\)th column gives the superclasses of the \(i\)th class. Here the element in position (1,2) is non-zero, so "list" is the superclass of "objectPad":

adjacencyOfClasses("gbutils", result = "adjacencyMatrix")
##: $vertices
##: [1] "objectPad" "list"     ##: $AM
##:           objectPad list
##: objectPad         0    1
##: list              0    0

Note that including the vertices in the result is not redundant, since some may not be in any edge. This can happen if a class does not have any superclasses and subclasses.

As described above the result is not converted to a graph object but it can be fed to functions provided by a number of R packages.

An additional option is to use argument Wolfram. If Wolfram is TRUE, a suitable Mathematica command is printed. It can be evaluated in a Mathematica session (e.g., by copy/paste) to produce a graphical representation of the graph and/or be manipulated further by it. This feature is a side effect, the return value of adjacencyOfClasses is as controlled by the other arguments. For example, the return value below is as without argument "Wolfram" but, in addition, the printed line defines a Wolfram language graph in terms of its vertices and edges:

adjacencyOfClasses("gbutils", Wolfram = TRUE)
##: Graph[{objectPad,list}, {list -> objectPad}, VertexLabels -> Automatic] ##: $vertices
##: [1] "objectPad" "list"     ##: $edges
##: [1] "list -> objectPad"

Setting result = "adjacencyMatrix" in the last R command exports the graph in terms of its adjacency matrix:

adjacencyOfClasses("gbutils", Wolfram = TRUE, result = "adjacencyMatrix")
##: AdjacencyGraph[{objectPad,list}, {{0, 0},
##: {1, 0} }
##: , VertexLabels -> Automatic] ##: $vertices
##: [1] "objectPad" "list"     ##: $AM
##:           objectPad list
##: objectPad         0    1
##: list              0    0

Value

a list with some of the following components (as described in Details):

vertices: a character vector of S4 class names,
edges: the edges of the graph, in the format controlled by argument results (not present when result is equal to "adjacencyMatrix"),
AM: the adjacency matrix of the graph (present only when result is "adjacencyMatrix").

References

Gentleman R, Whalen E, Huber W, Falcon S (2017). graph: A package to handle graph data structures. R package version 1.56.0.

Hansen KD, Gentry J, Long L, Gentleman R, Falcon S, Hahne F, Sarkar D (2017). Rgraphviz: Provides plotting capabilities for R graph objects. R package version 2.22.0.

Maechler M (2015). classGraph: Construct Graphs of S4 Class Hierarchies. (partly based on code from Robert Gentleman) R package version 0.7-5, https://CRAN.R-project.org/package=classGraph.

Author

Georgi N. Boshnakov

Examples

adjacencyOfClasses("gbutils")
#> $vertices
#> [1] "objectPad" "list"     
#> 
#> $edges
#> [1] "list -> objectPad"
#> 
adjacencyOfClasses("gbutils", TRUE)
#> $vertices
#> [1] "objectPad" "list"      "vector"   
#> 
#> $edges
#> [1] "list -> objectPad" "vector -> list"   
#> 

adjacencyOfClasses("gbutils", FALSE, "matrixOfPairs")
#> $vertices
#> [1] "objectPad" "list"     
#> 
#> $edges
#>      [,1]   [,2]       
#> [1,] "list" "objectPad"
#> 
adjacencyOfClasses("gbutils", TRUE,  "matrixOfPairs")
#> $vertices
#> [1] "objectPad" "list"      "vector"   
#> 
#> $edges
#>      [,1]     [,2]       
#> [1,] "list"   "objectPad"
#> [2,] "vector" "list"     
#> 

adjacencyOfClasses("gbutils", FALSE, "adjacencyMatrix")
#> $vertices
#> [1] "objectPad" "list"     
#> 
#> $AM
#>           objectPad list
#> objectPad         0    1
#> list              0    0
#> 
adjacencyOfClasses("gbutils", TRUE,  "adjacencyMatrix")
#> $vertices
#> [1] "objectPad" "list"      "vector"   
#> 
#> $AM
#>           objectPad list vector
#> objectPad         0    1      0
#> list              0    0      1
#> vector            0    0      0
#> 

## as above, also represent the graph using the edges
adjacencyOfClasses("gbutils", Wolfram = TRUE)
#> Graph[{objectPad,list}, {list -> objectPad}, VertexLabels -> Automatic] 
#> 
#> $vertices
#> [1] "objectPad" "list"     
#> 
#> $edges
#> [1] "list -> objectPad"
#> 
adjacencyOfClasses("gbutils", TRUE, Wolfram = TRUE)
#> Graph[{objectPad,list,vector}, {list -> objectPad, vector -> list}, VertexLabels -> Automatic] 
#> 
#> $vertices
#> [1] "objectPad" "list"      "vector"   
#> 
#> $edges
#> [1] "list -> objectPad" "vector -> list"   
#> 

## here the graph is represented by the adjacency matrix: 
adjacencyOfClasses("gbutils", FALSE, "adjacencyMatrix", Wolfram = TRUE)
#> AdjacencyGraph[{objectPad,list}, {{0, 0},
#> {1, 0} }
#> , VertexLabels -> Automatic] 
#> 
#> $vertices
#> [1] "objectPad" "list"     
#> 
#> $AM
#>           objectPad list
#> objectPad         0    1
#> list              0    0
#> 
adjacencyOfClasses("gbutils", TRUE,  "adjacencyMatrix", Wolfram = TRUE)
#> AdjacencyGraph[{objectPad,list,vector}, {{0, 0, 0},
#> {1, 0, 0},
#> {0, 1, 0} }
#> , VertexLabels -> Automatic] 
#> 
#> $vertices
#> [1] "objectPad" "list"      "vector"   
#> 
#> $AM
#>           objectPad list vector
#> objectPad         0    1      0
#> list              0    0      1
#> vector            0    0      0
#> 

if(requireNamespace("graph", quietly = TRUE) &&
   requireNamespace("Rgraphviz", quietly = TRUE)) withAutoprint({
    ## another package
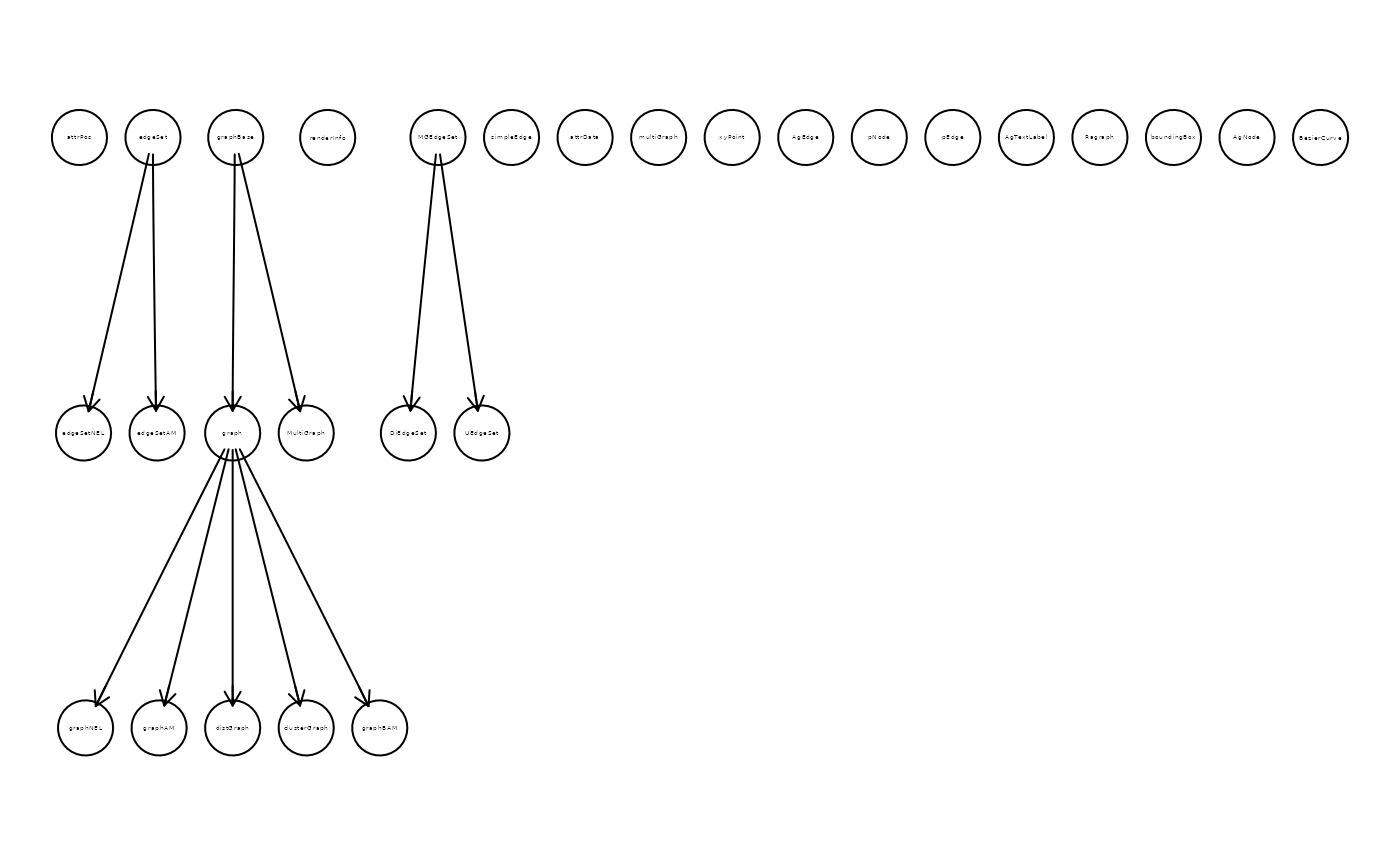
    adjacencyOfClasses("graph")
    ac1 <- adjacencyOfClasses("graph", FALSE, "adjacencyMatrix")
    ## note the use of t() below
    gr_ac1 <- graph::graphAM(adjMat = t(ac1$AM), edgemode = "directed")
    if(require("Rgraphviz", quietly = TRUE, warn.conflicts = FALSE))
        plot(gr_ac1)
    ## more than one package
    ac2 <- adjacencyOfClasses(c("graph", "Rgraphviz"), FALSE, "adjacencyMatrix")
    gr_ac2 <- graph::graphAM(adjMat = t(ac2$AM), edgemode = "directed")
    if(require("Rgraphviz", quietly = TRUE))
        plot(gr_ac2)
})
#> > adjacencyOfClasses("graph")
#> $vertices
#>  [1] "attrPos"      "edgeSet"      "graphBase"    "renderInfo"   "MGEdgeSet"   
#>  [6] "MultiGraph"   "UEdgeSet"     "simpleEdge"   "graphAM"      "graphBAM"    
#> [11] "clusterGraph" "attrData"     "multiGraph"   "distGraph"    "edgeSetAM"   
#> [16] "DiEdgeSet"    "edgeSetNEL"   "graphNEL"     "graph"       
#> 
#> $edges
#>  [1] "edgeSet -> edgeSetNEL"   "edgeSet -> edgeSetAM"   
#>  [3] "graphBase -> graph"      "graphBase -> MultiGraph"
#>  [5] "graph -> graphNEL"       "graph -> graphAM"       
#>  [7] "graph -> distGraph"      "graph -> clusterGraph"  
#>  [9] "graph -> graphBAM"       "MGEdgeSet -> DiEdgeSet" 
#> [11] "MGEdgeSet -> UEdgeSet"  
#> 
#> > ac1 <- adjacencyOfClasses("graph", FALSE, "adjacencyMatrix")
#> > gr_ac1 <- graph::graphAM(adjMat = t(ac1$AM), edgemode = "directed")
#> > if (require("Rgraphviz", quietly = TRUE, warn.conflicts = FALSE)) plot(gr_ac1)
#> 
#> Attaching package: ‘BiocGenerics’
#> The following objects are masked from ‘package:stats’:
#> 
#>     IQR, mad, sd, var, xtabs
#> The following objects are masked from ‘package:base’:
#> 
#>     Filter, Find, Map, Position, Reduce, anyDuplicated, append,
#>     as.data.frame, basename, cbind, colnames, dirname, do.call,
#>     duplicated, eval, evalq, get, grep, grepl, intersect, is.unsorted,
#>     lapply, mapply, match, mget, order, paste, pmax, pmax.int, pmin,
#>     pmin.int, rank, rbind, rownames, sapply, setdiff, sort, table,
#>     tapply, union, unique, unsplit, which.max, which.min

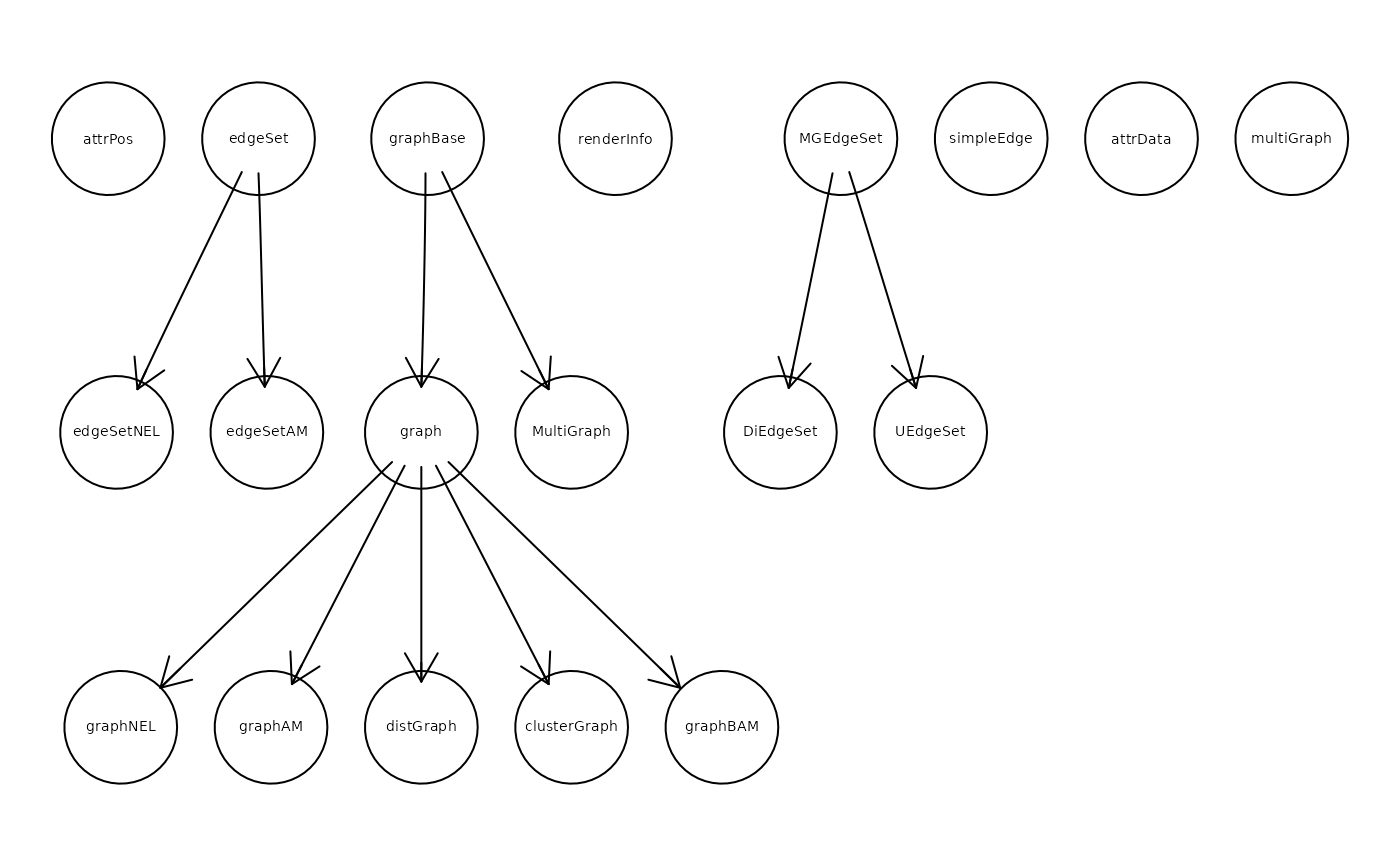#> > ac2 <- adjacencyOfClasses(c("graph", "Rgraphviz"), FALSE, "adjacencyMatrix")
#> > gr_ac2 <- graph::graphAM(adjMat = t(ac2$AM), edgemode = "directed")
#> > if (require("Rgraphviz", quietly = TRUE)) plot(gr_ac2)