Multi-step predictions for MixAR models

Multi-step predictions for MixAR models.

Usage

multiStep_dist(model, maxh, N, xcond, ...)

Arguments

model: a MixAR model.
maxh: maximal horizon, a positive integer.
N: an integer specifying the number of simulation samples to use, see 'Details. This argument is used only by simulation based methods.
xcond: the past values needed for the conditional distribution, a numeric vector of length at least the maximal AR order of the components.
...: used only in some methods, see the details for the individual methods.

Details

The function currently implements two methods: the exact method due to Boshnakov (2009) and a simulation method described by (Wong and Li 2000) for Gaussian MixAR models but valid more generally.

The simulation method is available for any MixAR model, while the exact method is currently implemented only for models with Gaussian components ("MixARGaussian" class).

multiStep_dist returns a function which can be used to obtain various properties of the predictive distribution for lags up to maxh.

If argument N is missing the exact method is tried. Currently an error will result if the exact method is not implemented for model.

If argument N is given it must be a scalar numeric value, the number of simulations to be performed to construct an approximation for the predictive distributions.

The simulation is done by multiStep_dist. The properties obtained later from the function returned by multiStep_dist use the samples generated by the call to multiStep_dist. To do a simulation with different parameters (e.g., with larger N) call multiStep_dist again.

Details on the returned function

If xcond is missing multiStep_dist returns a function with arguments h, what and xcond. If xcond is supplied, then it is fixed to that value and the arguments of the returned function are h, what and '...'. The dots argument is currently used in the case of the simulation method, see below.

Let f be the function returned by multiStep_dist. Argument h is the required prediction horizon and can be a number in the interval \([1,maxh]\). Argument what is the required property of the predictive distribution for lag h. If what is a function, it is applied to the simulated sample for the requested horizon (currently available only for the simulation method). If what is a character string, the corresponding property of the predictive distribution for horizon h is returned. Currently possible values for what are:

"pdf": the probability density function.
"cdf": the cumulative distribution function.
"location": the location (conditional mean).
"variance": the conditional variance, a.k.a (squared) volatility.
"sd": the conditional standard deviation, a.k.a volatility.
"skewness": the conditional skewness.
"kurtosis": the conditional kurtosis.

Note that what = "pdf" and what = "cdf" return functions even in the simulation case. For "pdf" the function is constructed using density and the "..." arguments passed to f will be passed on to density if finer control is needed.

If what is none of the above, the raw object is returned currently (but this may change).

Value

a function as described in sections ‘Details’ and ‘Methods’

Methods

The Details section gives a rather detailed description of the function, so the descriptions below are brief.

signature(model = "MixAR", maxh = "numeric", N = "numeric", xcond = "numeric"): Non-missing N requests the simulation method. The predictive distribution is approximated by simulating N of future paths up to horizon maxh and using a non-parametric estimate. Arguments "..." are passed to density to allow finer control.
signature(model = "MixARGaussian", maxh = "numeric", N = "missing", xcond = "missing"): Computes the predictive distribution using the exact method. Returns a function with arguments h, what and xcond.
signature(model = "MixARGaussian", maxh = "numeric", N = "missing", xcond = "ANY"): Computes the predictive distribution using the exact method. Returns a function with arguments h and what. (i.e., xcond is fixed to the supplied argument xcond).

References

Boshnakov GN (2009). “Analytic expressions for predictive distributions in mixture autoregressive models.” Stat. Probab. Lett. , 79(15), 1704-1709. doi:10.1016/j.spl.2009.04.009 .

Wong CS, Li WK (2000). “On a mixture autoregressive model.” J. R. Stat. Soc., Ser. B, Stat. Methodol. , 62(1), 95-115.

Author

Georgi N. Boshnakov

Examples

## exact method, without xcond
dist <- multiStep_dist(exampleModels$WL_ibm, maxh = 3)

tfpdf <- dist(3, "pdf", xcond = c(560, 600)) # xcond is argument to 'dist' here
tfcdf <- dist(3, "cdf", xcond = c(560, 600))
## plot the pdf (gbutils::plotpdf determines suitable range automatically)
gbutils::plotpdf(tfpdf, cdf = tfcdf)

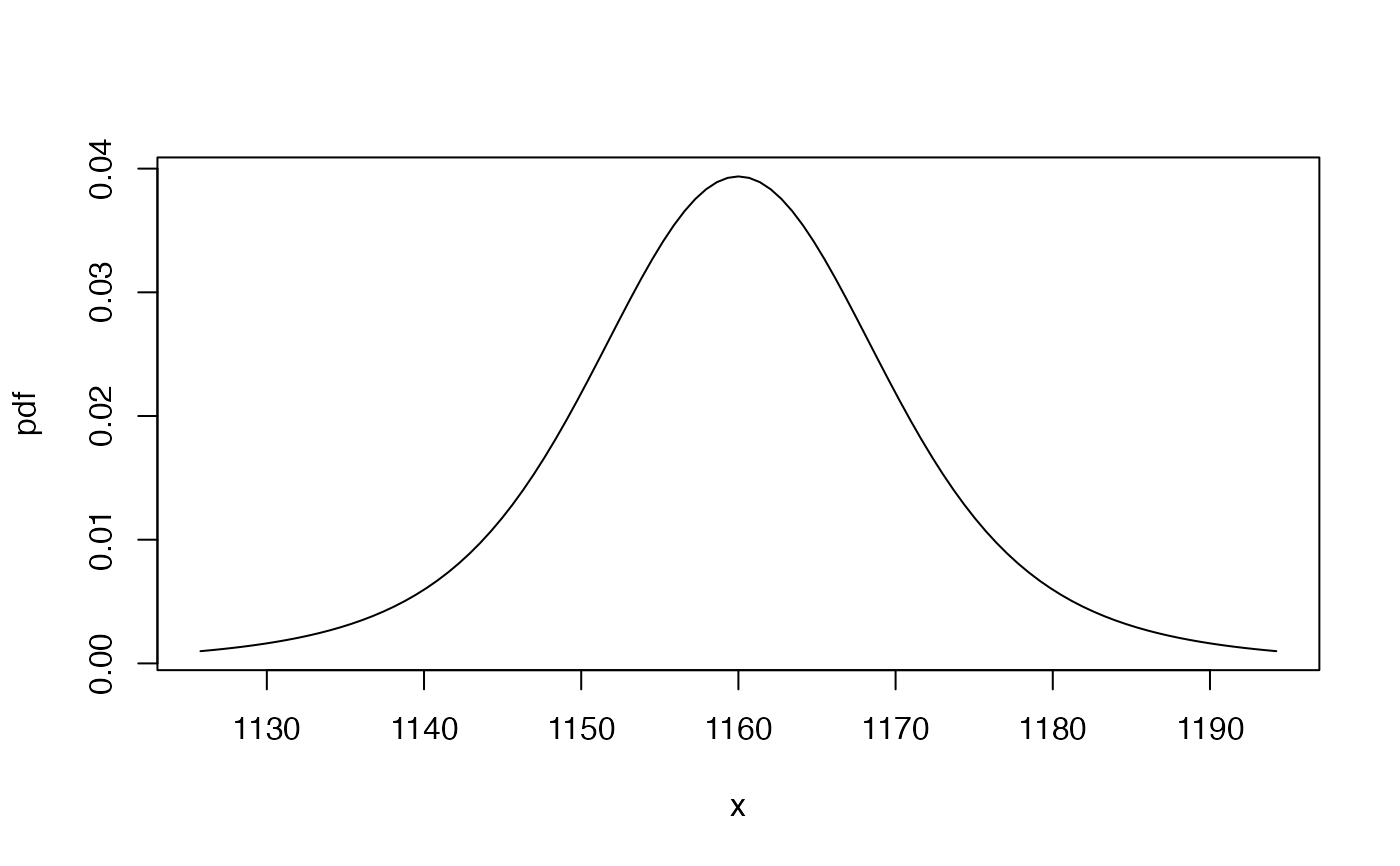args(dist(3, "pdf", xcond = c(500, 600)))  # x
#> function (x) 
#> NULL

## use a simulation method with N = 1000
tf  <- multiStep_dist(exampleModels$WL_ibm, maxh = 3, N = 1000, xcond = c(560, 600))
args(tf) # (h, what, ...)
#> function (h, what, ...) 
#> NULL

## the exact method may also be used with fixed xcond:
tfe <- multiStep_dist(exampleModels$WL_ibm, maxh = 3, xcond = c(560, 600))

## get pdf and cdf for horizon 3
tfepdf <- tfe(3, "pdf")
tfecdf <- tfe(3, "cdf")
## plot the pdf
gbutils::plotpdf(tfepdf, cdf = tfecdf)


tf(3, "location")
#> [1] 605.4452

tf(1, "location")
#> [1] 605.0603
mix_location(exampleModels$WL_ibm, xcond = c(560, 600))
#> [1] 604.2307

## larger simulation gives better approximation, in general
tf <- multiStep_dist(exampleModels$WL_ibm, maxh = 3, N = 10000, xcond = c(560, 600))
tf(1, "location")
#> [1] 604.1339

tf1000pdf <- tf(3, "pdf")
tf1000cdf <- tf(3, "cdf")
gbutils::plotpdf(tf1000pdf, cdf = tf1000cdf)


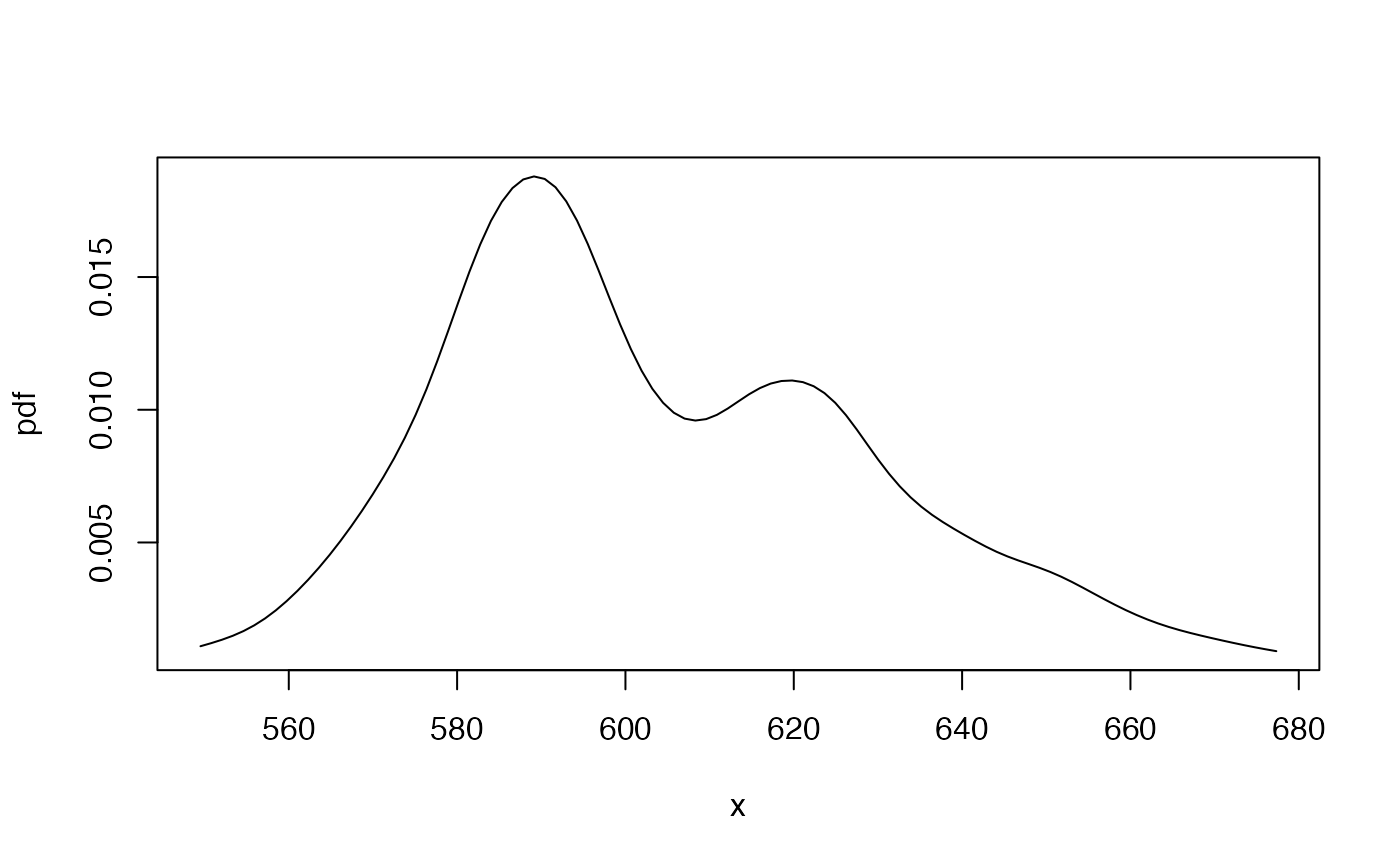## plot the exact and simulated pdf's together for comparison
gbutils::plotpdf(tfepdf, cdf = tfecdf)
curve(tf1000pdf, add = TRUE, col = "red")


## get the raw data
tfs <- tf(1, "sampled")
apply(tfs, 2, mean) # location for lags from 1 to maxh (here 3)
#> [1] 604.1339 604.3950 604.3542

tf(1, "location")
#> [1] 604.1339
tf(1, "variance")
#> [1] 412.8627
tf(1, "sd")
#> [1] 20.31902
mix_variance(exampleModels$WL_ibm, xcond = c(560, 600))
#> [1] 413.0203
sqrt(mix_variance(exampleModels$WL_ibm, xcond = c(560, 600)))
#> [1] 20.3229

mix_kurtosis(exampleModels$WL_ibm, xcond = c(359, 200))
#> [1] 1.135385
mix_kurtosis(exampleModels$WL_ibm, xcond = c(359, 400))
#> [1] 1.392797