Turning points of a time series — turns • timeSeries

Extracts and analyzes turning points of an univariate "timeSeries" object.

Usage

turns(x, ...)

turnsStats(x, doplot = TRUE)

Arguments

x: an univariate "timeSeries" object of financial indices or prices.
...: optional arguments passed to the function na.omit.
doplot: a logical flag, should the results be plotted? By default TRUE.

Details

The function turns determines the number and the positions of extrema (turning points, either peaks or pits) in a regular time series.

The function turnsStats calculates the quantity of information associated with the observations in this series, according to Kendall's information theory.

The functions are borrowed from the contributed R package pastecs and made ready for working together with univariate timeSeries objects. You need not to load the R package pastecs, the code parts we need here are builtin in the timeSeries package.

We have renamed the function turnpoints to turns to distinguish between the original function in the contributed R package pastecs and our Rmetrics function wrapper.

For further details please consult the help page from the contributed R package pastecs.

Value

for turns, an object of class timeSeries.

for turnsStats, an object of class turnpoints with the following entries:

data: The dataset to which the calculation is done.
n: The number of observations.
points: The value of the points in the series, after elimination of ex-aequos.
pos: The position of the points on the time scale in the series (including ex-aequos).
exaequos: Location of exaequos (1), or not (0).
nturns: Total number of turning points in the whole time series.
firstispeak: Is the first turning point a peak (TRUE), or not (FALSE).
peaks: Logical vector. Location of the peaks in the time series without ex-aequos.
pits: Logical vector. Location of the pits in the time series without ex-aequos.
tppos: Position of the turning points in the initial series (with ex-aequos).
proba: Probability to find a turning point at this location.
info: Quantity of information associated with this point.

Author

Frederic Ibanez and Philippe Grosjean for code from the contributed R package pastecs and Rmetrics for the function wrapper.

References

Ibanez, F., 1982, Sur une nouvelle application de la theorie de l'information a la description des series chronologiques planctoniques. J. Exp. Mar. Biol. Ecol., 4, 619--632

Kendall, M.G., 1976, Time Series, 2nd ed. Charles Griffin and Co, London.

Examples

## Load Swiss Equities Series -  
   SPI.RET <- LPP2005REC[, "SPI"]
   head(SPI.RET)
#> GMT 
#>                     SPI
#> 2005-11-01  0.008414595
#> 2005-11-02  0.002519342
#> 2005-11-03  0.012707292
#> 2005-11-04 -0.000702757
#> 2005-11-07  0.006205226
#> 2005-11-08  0.000329260

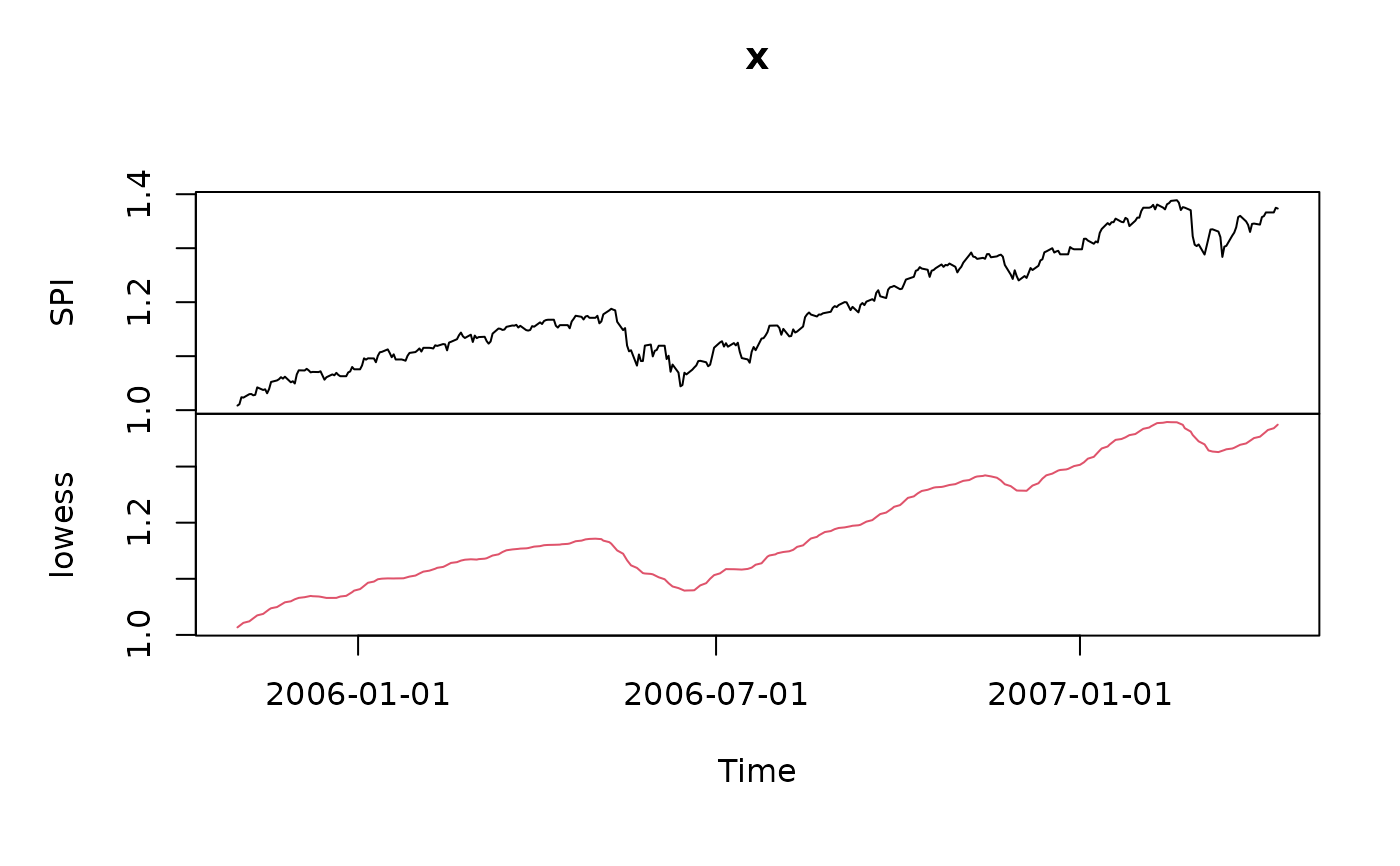
## Cumulate and Smooth the Series -
   SPI <- smoothLowess(cumulated(SPI.RET), f=0.05)
   plot(SPI)

   
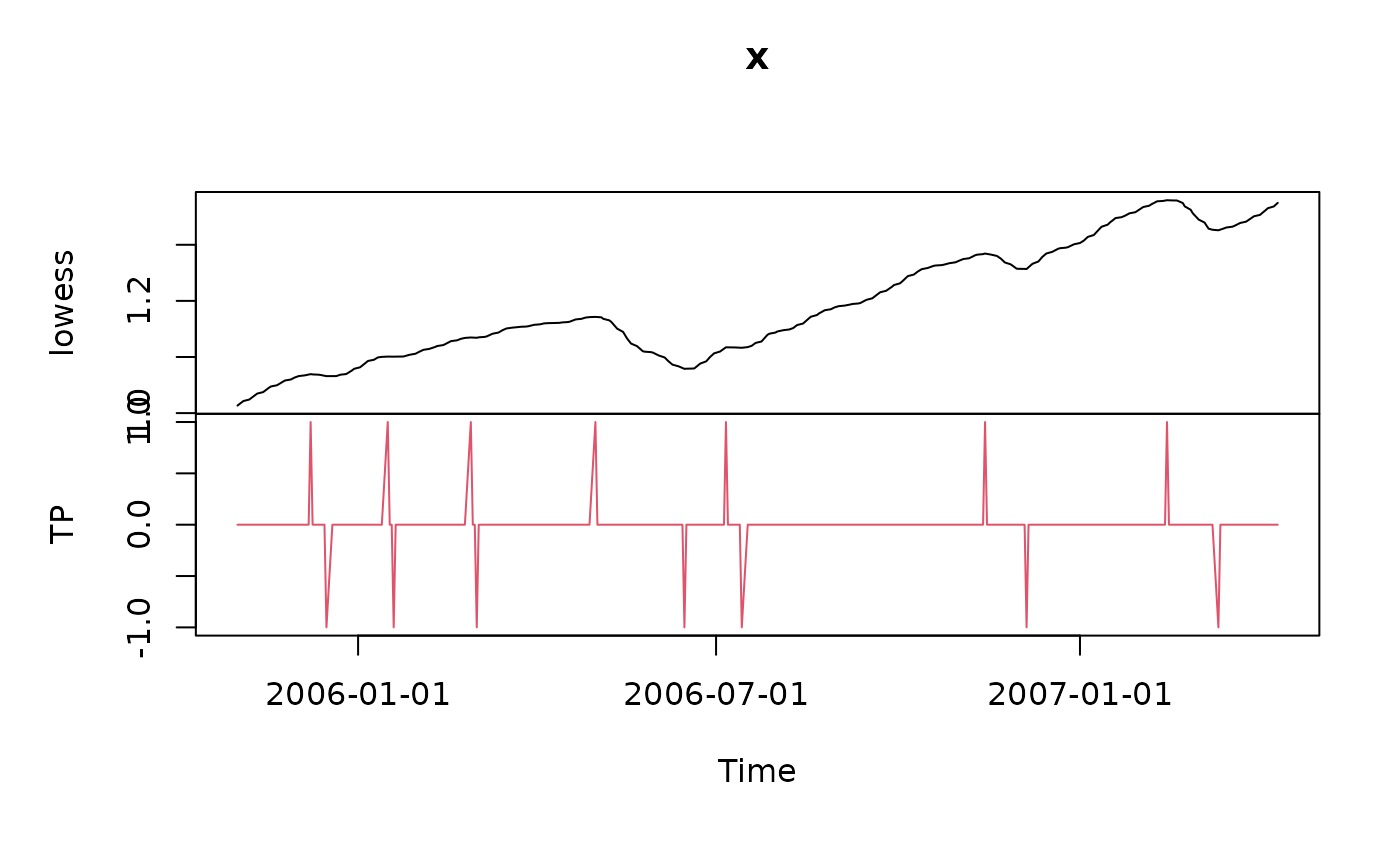
## Plot Turn Points Series - 
   SPI.SMOOTH <- SPI[, 2]
   tP <- turns(SPI.SMOOTH)
   plot(tP)

   
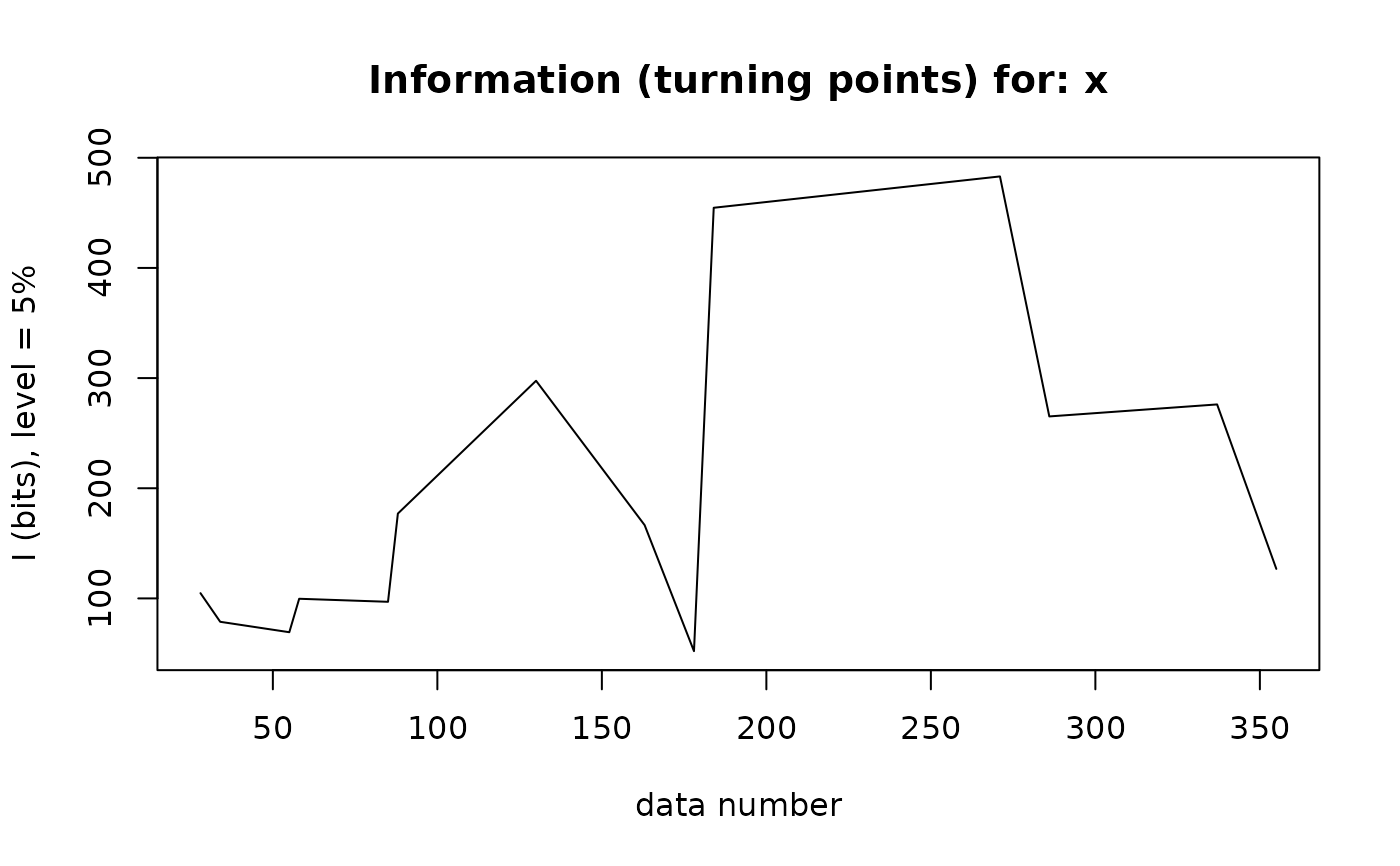
## Compute Statistics -
   turnsStats(SPI.SMOOTH)
#> Turning points for: x 
#> 
#> nbr observations  : 377 
#> nbr ex-aequos     : 0 
#> nbr turning points: 14 (first point is a peak)
#> E(p) = 250 Var(p) = 66.7 (theoretical)
#> 
#>    point type         proba      info
#> 1     28 peak  2.894020e-32 104.76862
#> 2     34  pit  1.941760e-24  78.76891
#> 3     55 peak  1.370106e-21  69.30620
#> 4     58  pit  9.874935e-31  99.67600
#> 5     85 peak  6.665581e-30  96.92111
#> 6     88  pit  5.157541e-54 177.01743
#> 7    130 peak  2.664544e-90 297.55964
#> 8    163  pit  7.413829e-51 166.52811
#> 9    178 peak  2.069038e-16  52.10189
#> 10   184  pit 1.402003e-137 454.61666
#> 11   271 peak 3.830644e-146 483.06391
#> 12   286  pit  1.471670e-80 265.19679
#> 13   337 peak  7.722581e-84 276.09288
#> 14   355  pit  6.778577e-39 126.79421