Computations for Lectures W7a-W8b - Practical Statistics I (2016/2017)

Edited examples from the lectures

Georgi N. Boshnakov

March 2017

Packages and functions for topic “goodness of fit”

Functions in base R

?ks.test
?ecdf
?qqnorm
?qqline

Package “psistat”

Package psistat provides some useful functions for this topic. You can install it on your own computers from the web page of the course (if you have not done this yet).

library(psistat)

The names of the functions in “psistat” start with “psi.”. You can learn more about them using the help system. For example:

apropos("psi.*")
help(package="psistat")
package ? psistat
?psi.eqf
?psi.Dn
?psi.lks.exp.test
?psi.jitter

Other libraries providing relevant functions:

library(nortest) # for Lilliefors test
?lillie.test
library(e1071)  # for probplot
?probplot

Dataset Oxboys is in package “mlmRev”

library(mlmRev)
# ?Oxboys

Miscellaneous: use this command to plot in a new window:

Some random samples for the following examples.

x20 <- rnorm(20)            # a short random sample, to show it on screen
x200 <- rnorm(200)          # larger
x500 <- rnorm(500)          # even larger
x500ms <- rnorm(500, mean = 1, sd = 3)

x2 <- rchisq(100, df = 2)

xe <- rexp(500, rate = 1/1500) # life times of electric bulbs

Empirical cdf (ecdf)

x20.ecdf <- ecdf(x20)              # its ecdf
x20.ecdf
## Empirical CDF 
## Call: ecdf(x20)
##  x[1:20] = -2.3457, -1.2071, -0.99839,  ..., 1.0844, 2.4158

x20.ecdf is a function - we can use it as any other R function:

x20.ecdf(0)
## [1] 0.65
x20.ecdf(10)
## [1] 1

Here we plot the ecdf and overlay the cdf used to simulate the data. The sample is small, so the two do not match very closely:

plot(x20.ecdf)
curve(pnorm, add = TRUE, col = "blue")

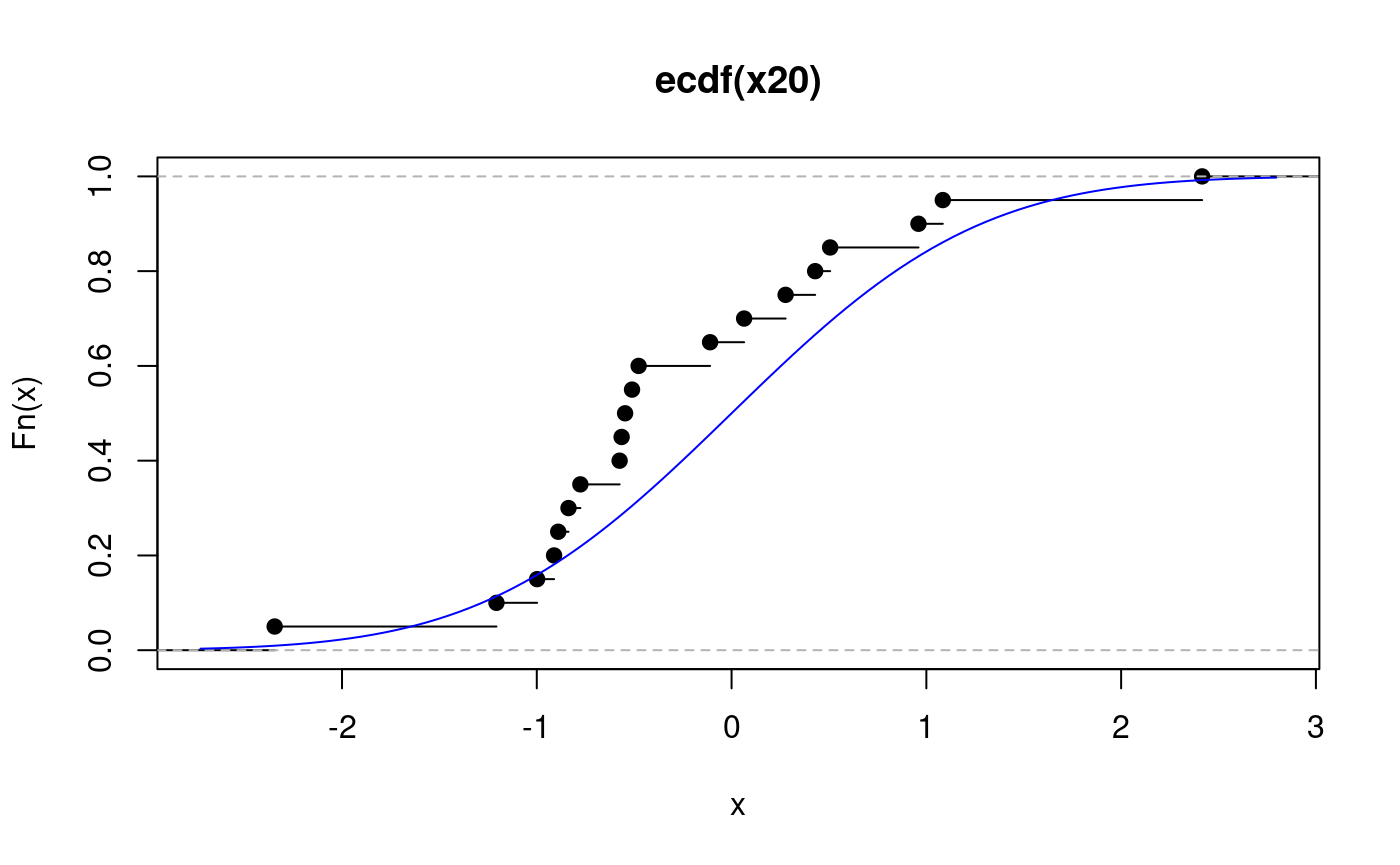
At the places were the ecdf jumps, the value is the one after the jump (indicated by the filled points). Here is a histogram with overlayed pdf for comparison.

hist(x20, freq = FALSE, ylim = c(0, 0.5))
curve(dnorm, add = TRUE)

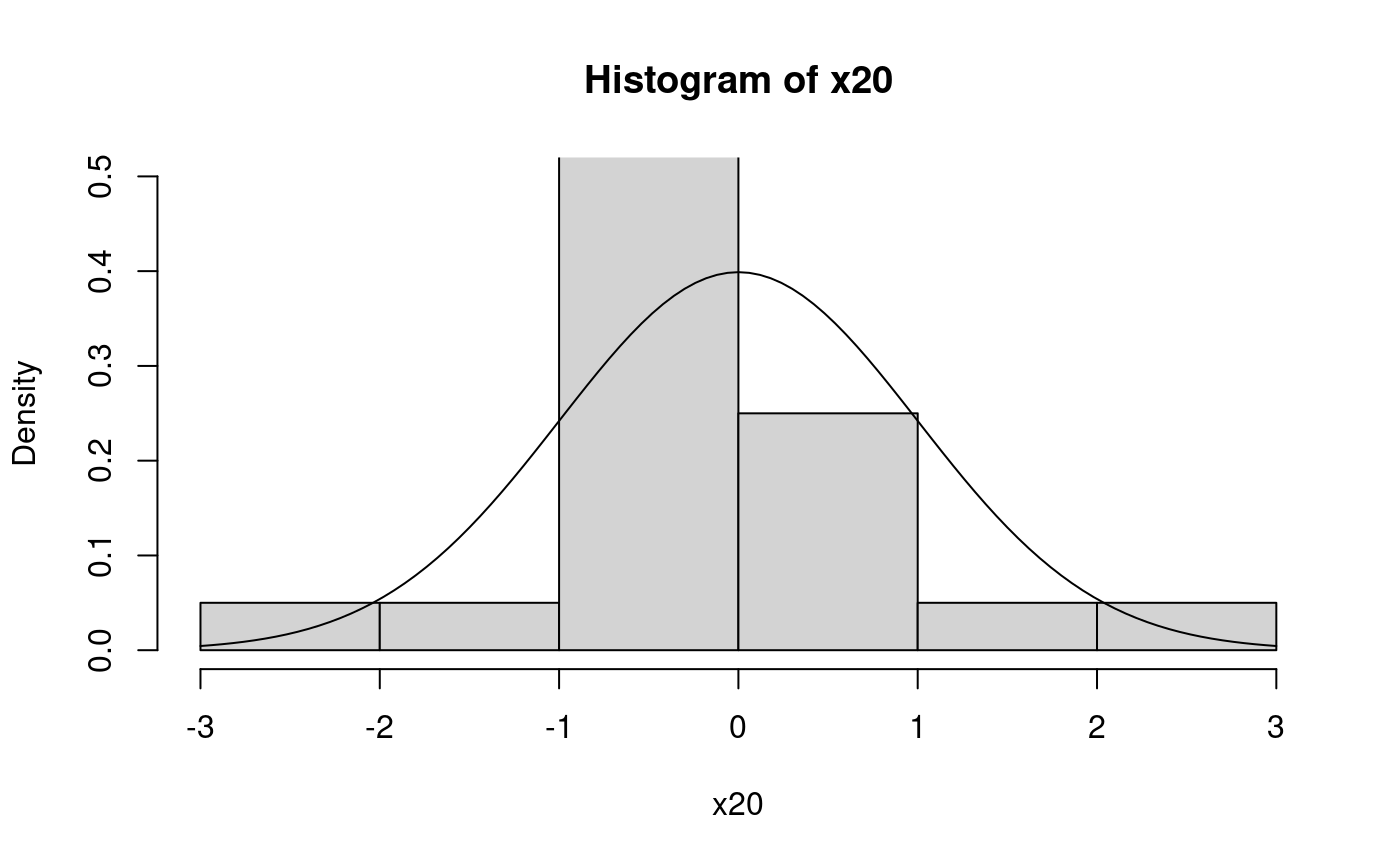
For larger samples the ecdf is very good estimator of the underlying cdf:

x200.ecdf <- ecdf(x200)
plot(x200.ecdf)
curve(pnorm, add = TRUE, col = "red")

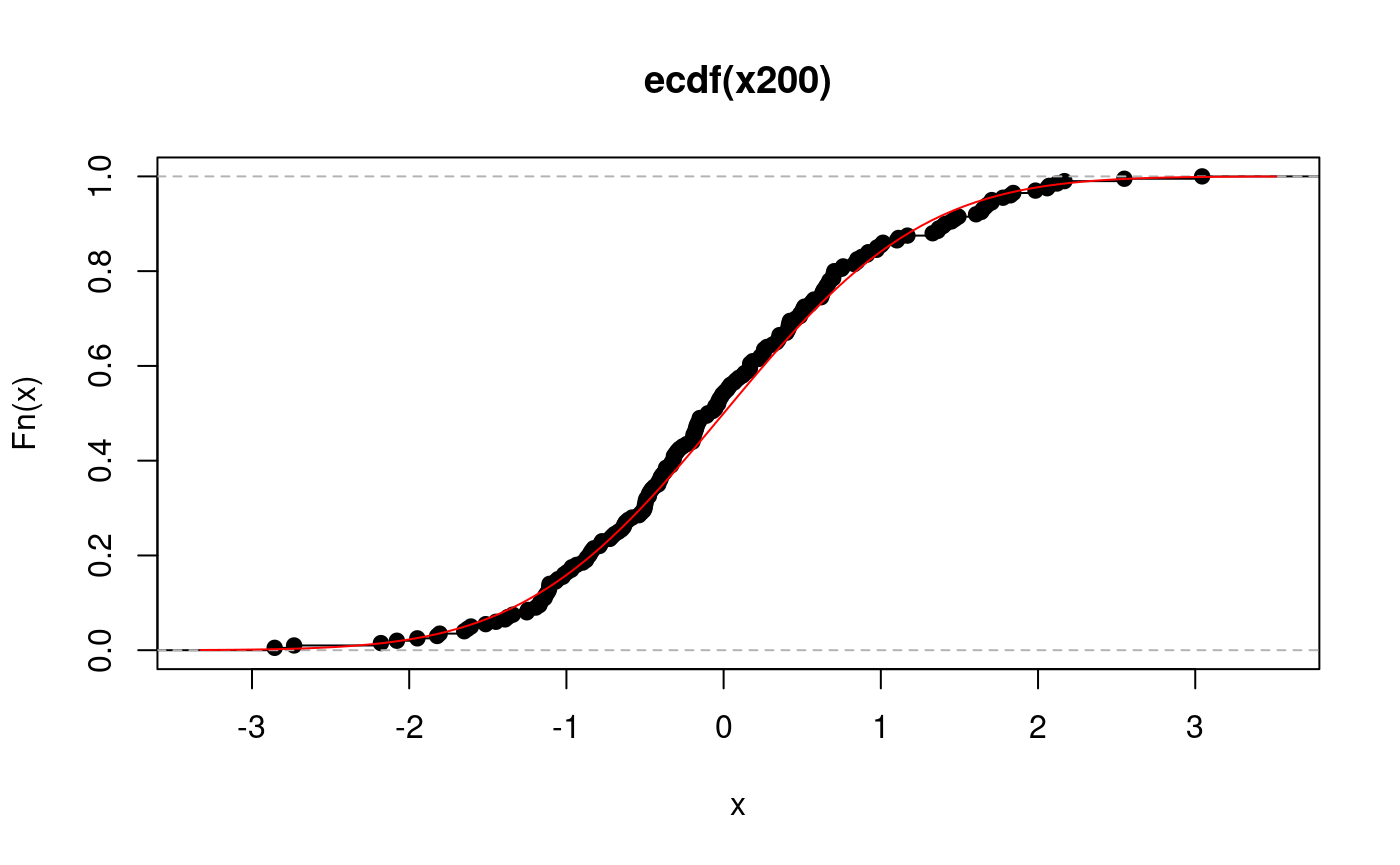
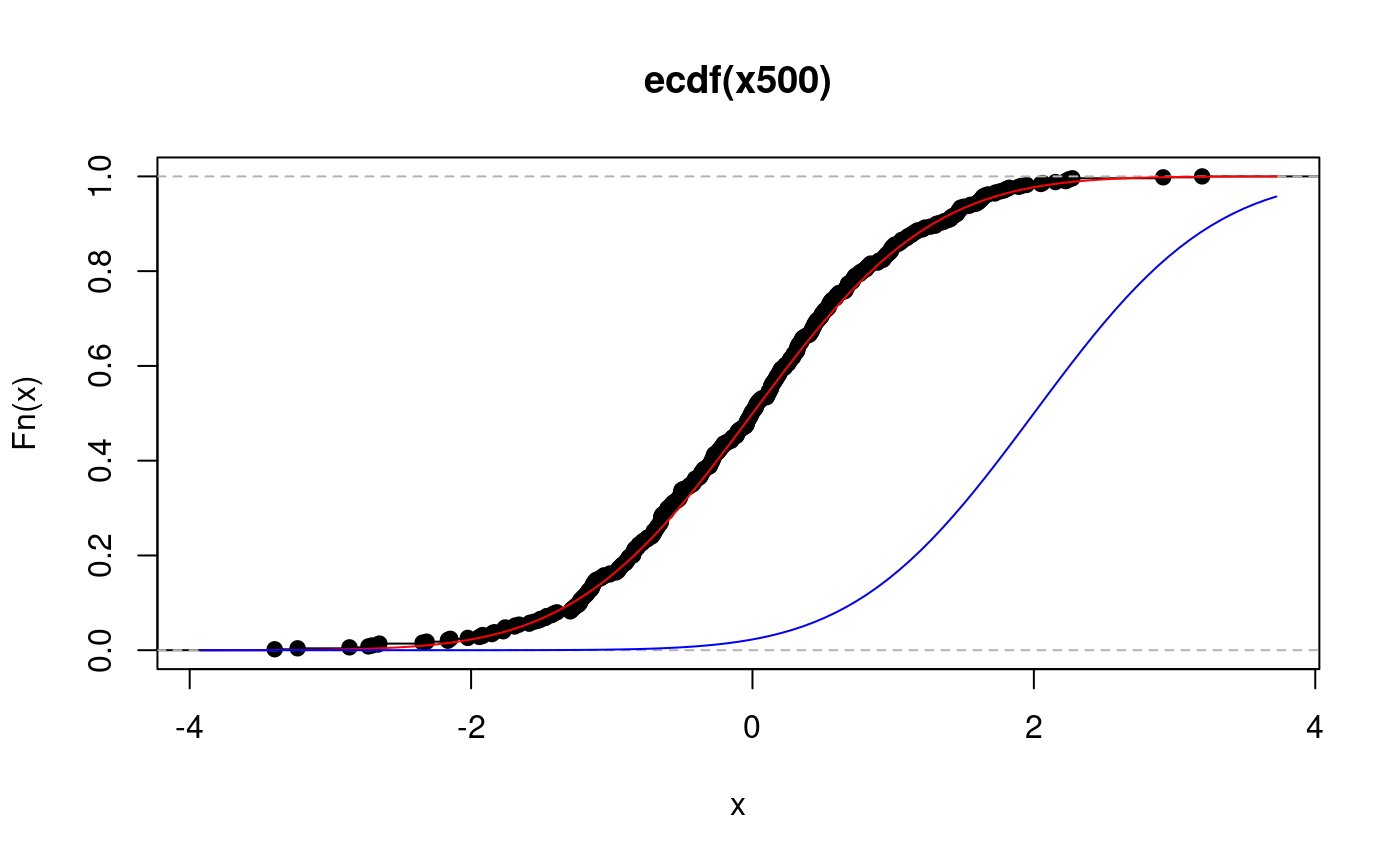
… and an even larger sample:

x500.ecdf <- ecdf(x500)            # its ecdf
plot(x500.ecdf)                    # ecdf and cdf overlayed
curve(pnorm, add = TRUE, col = "red")
## This shows how to add the curve with non-default values of the
## arguments. This simply illustrates the technique:
norm2 <- function(x) pnorm(x, mean = 2)
curve(norm2, add = TRUE, col = "blue")

Empirical quantiles

# ?quantile
quantile(x500, probs=0.5)
##          50% 
## -0.005702427
quantile(x500, probs= c(0.25,0.5, 0.75))
##          25%          50%          75% 
## -0.700895608 -0.005702427  0.604292246
quantile(x20, 0.5)
##        50% 
## -0.5288207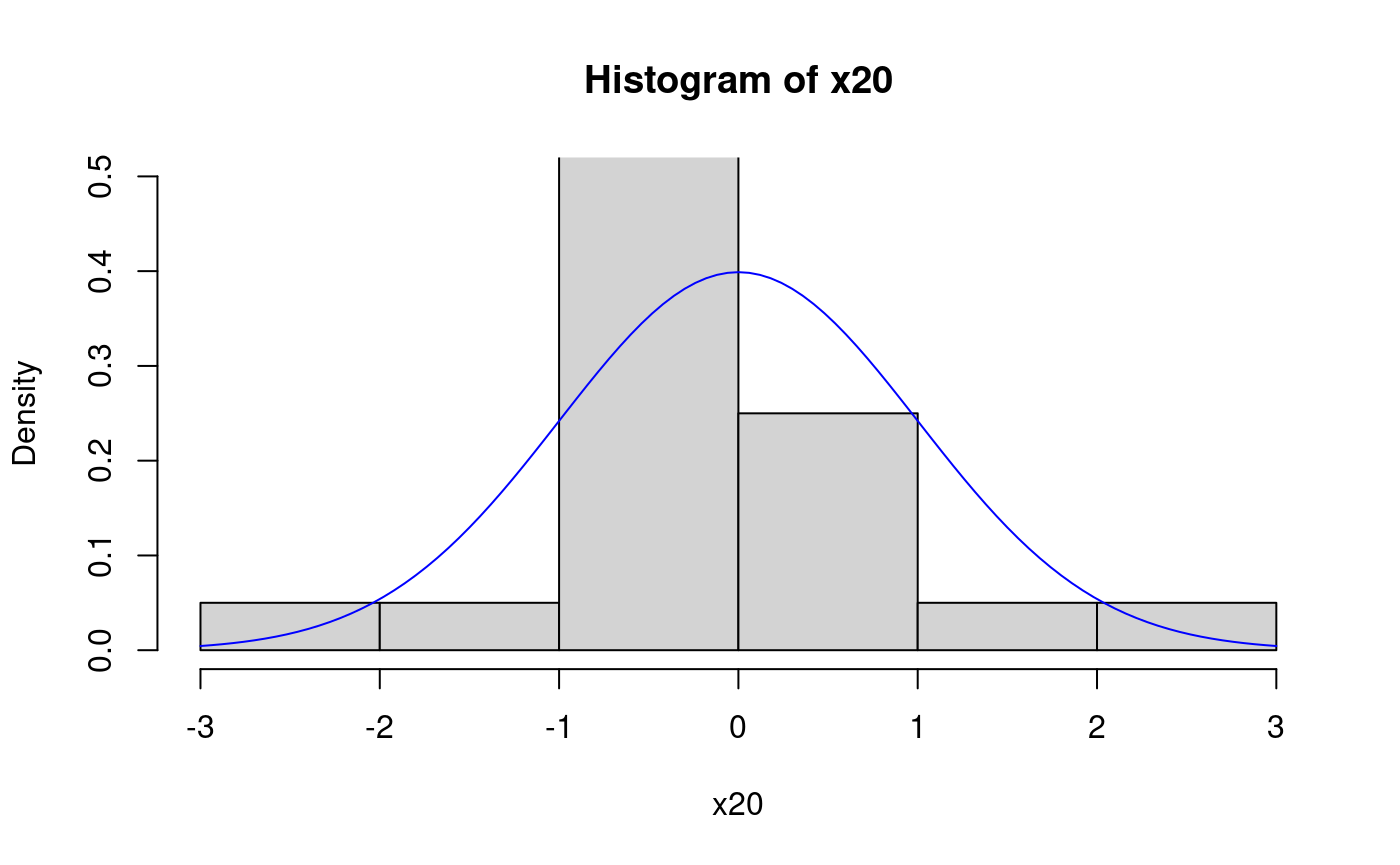
hist(x20, freq=FALSE, ylim = c(0, 0.5))
curve(dnorm, from = -3, to = 3,  add = TRUE, col = "blue")

Examples with psi.eqf

Empirical quantile function (from package “psistat”)

?psi.eqf

The eqf of a small sample:

x20.eqf <- psi.eqf(x20)
plot(x20.eqf, main = "Eqf of x20")
curve(qnorm, add = TRUE, col = "blue")
## Warning in qnorm(x): NaNs produced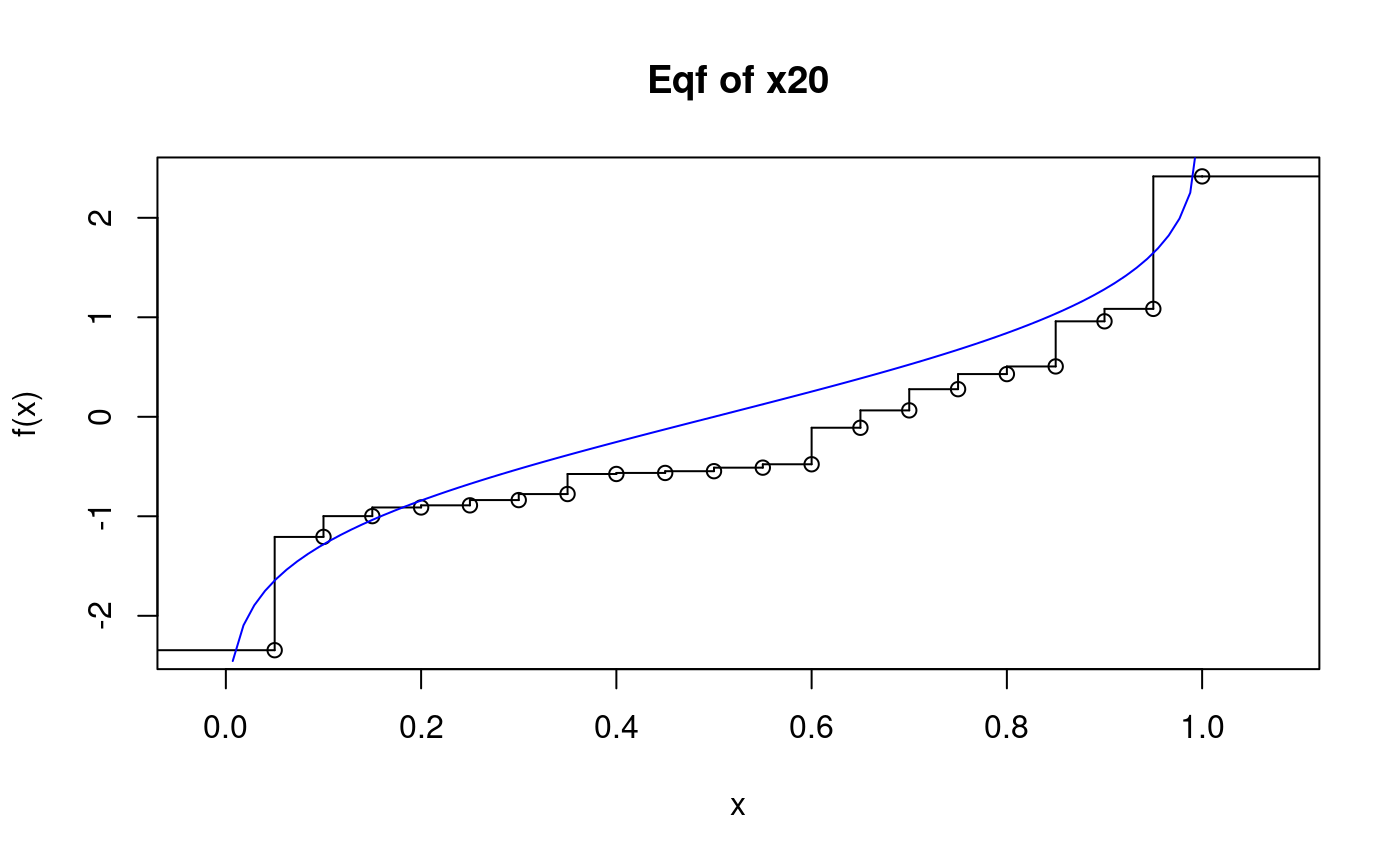

# plot(x200)
x200ecdf <- ecdf(x200)
x200ecdf(0)
## [1] 0.54
quantile(x200, c(.25, .5, 0.75))
##         25%         50%         75% 
## -0.65421071 -0.08424212  0.62585887
x200eqf <- psi.eqf(x200)
x200eqf(0.5)
## [1] -0.09979059
x200eqf(0.25)
## [1] -0.6696336
plot(x200eqf, main = "Eqf of x200")

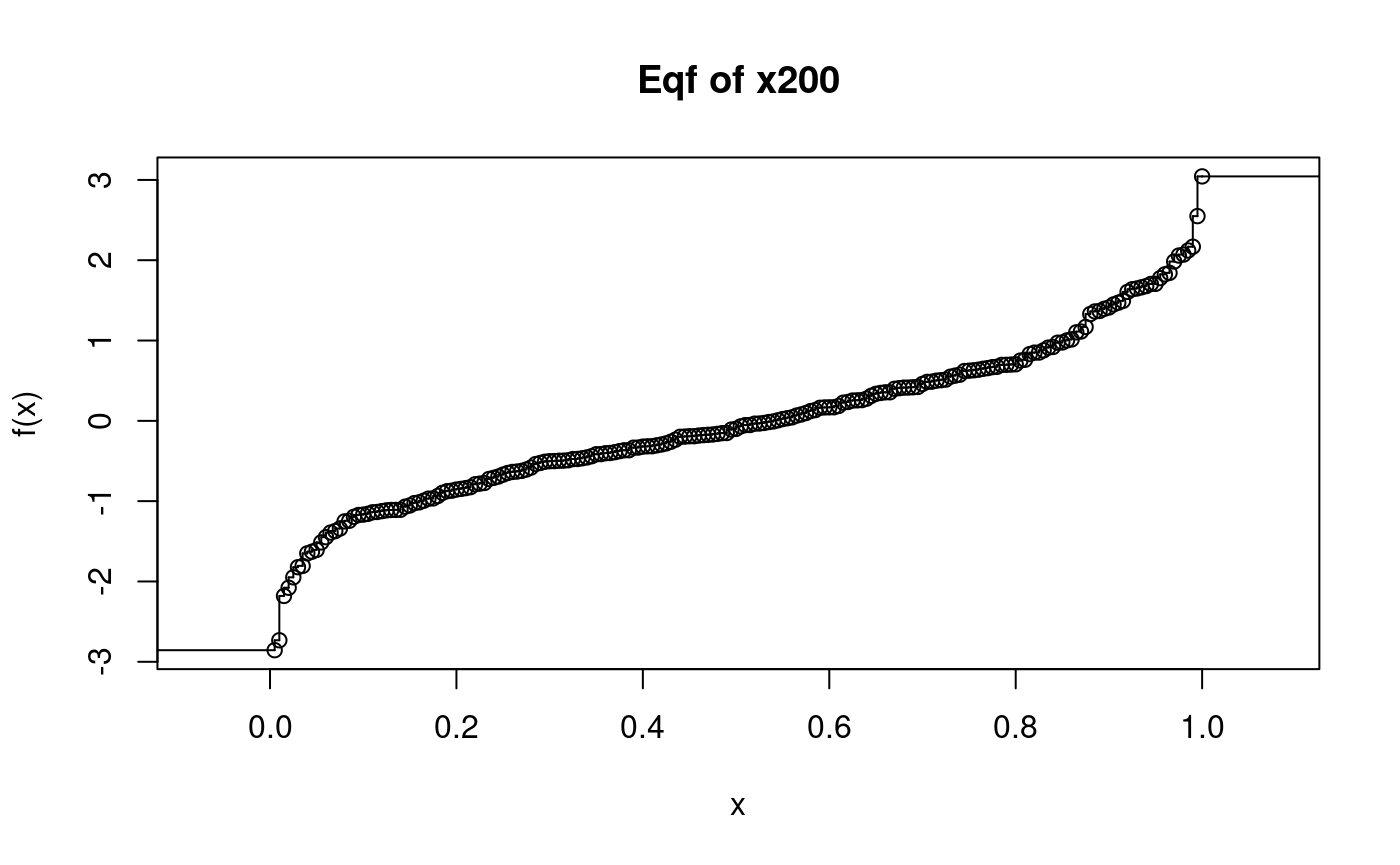
x500.eqf <- psi.eqf(x500)          # a larger sample
plot(x500.eqf, main = "Eqf of x500")
curve(qnorm, add = TRUE, col = "blue")
## Warning in qnorm(x): NaNs produced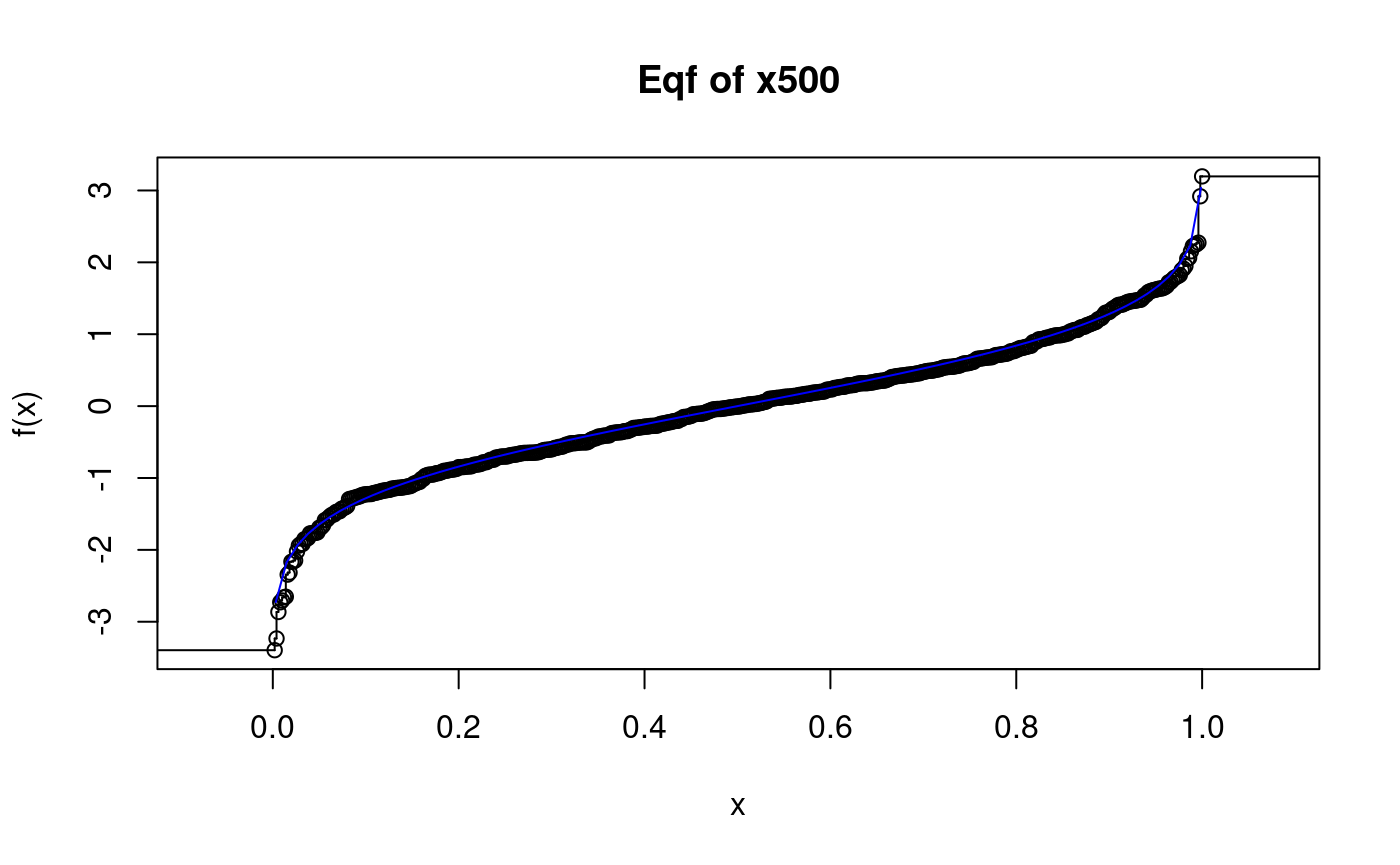

QQ-plots

DIY qq-plots

We follow the procedure given in the notes: prepare points p, evaluate the scores s, compute the order statistics and plot. Does x20 come from N(0,1)?

n <- length(x20)
n
## [1] 20
p <- (1:n - 0.5)   # to check that it gives 0.5, 1.5, ..., 19.5
p
##  [1]  0.5  1.5  2.5  3.5  4.5  5.5  6.5  7.5  8.5  9.5 10.5 11.5 12.5 13.5 14.5
## [16] 15.5 16.5 17.5 18.5 19.5
p <- (1:n - 0.5)/n
p
##  [1] 0.025 0.075 0.125 0.175 0.225 0.275 0.325 0.375 0.425 0.475 0.525 0.575
## [13] 0.625 0.675 0.725 0.775 0.825 0.875 0.925 0.975
s <- qnorm(p)            # scores
x20.sorted <- sort(x20)  # order statistics
plot(s, x20.sorted)      # qq-plot
abline(0, 1, col = "blue") # plot the reference line

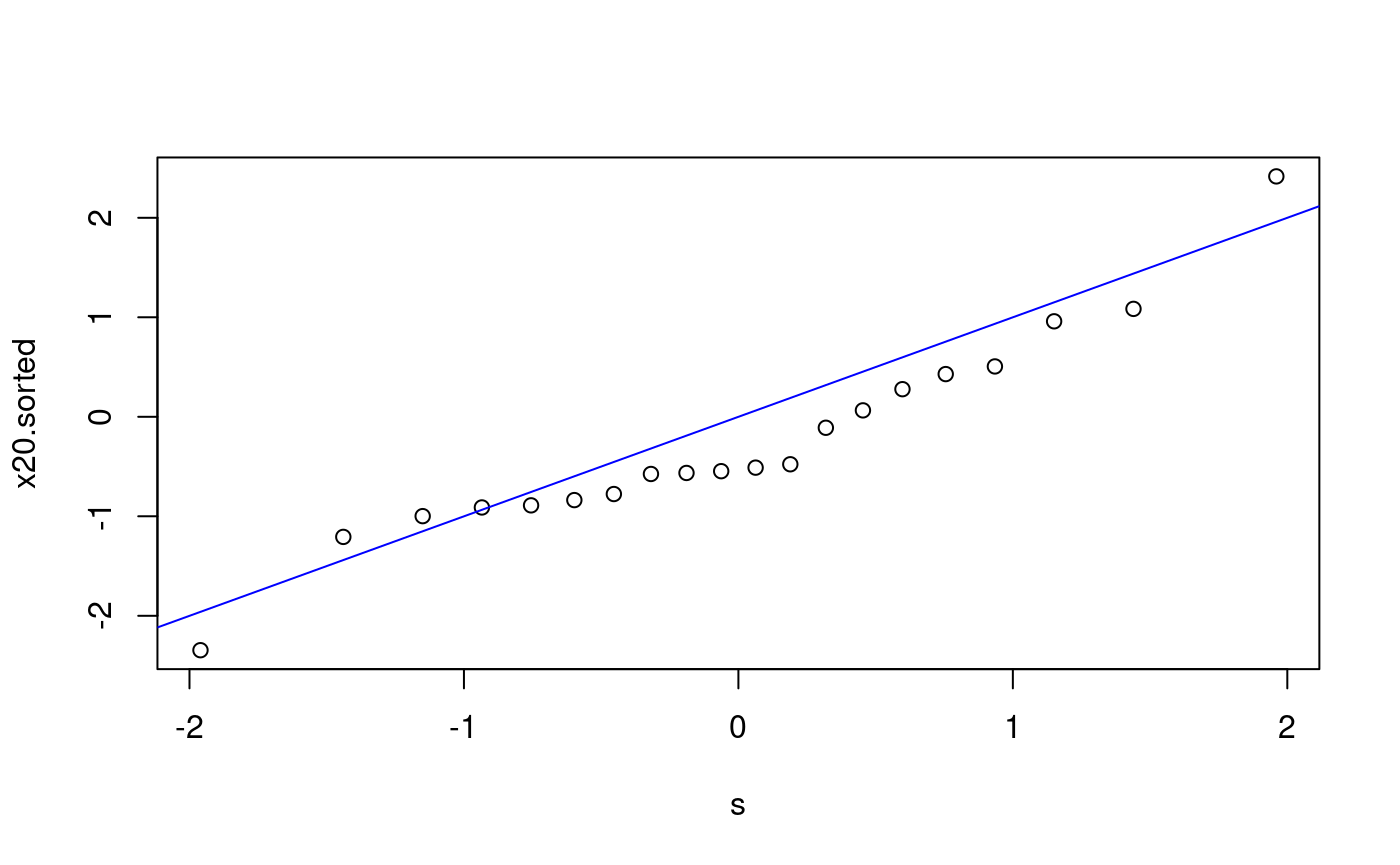
Does x2 come from N(0,1)?

n <- length(x2)
p <- ((1:n) - 0.5) / n
s2 <- qnorm(p)
x2s <- sort(x2)
plot(s2, x2s)
abline(0, 1, col = "red")

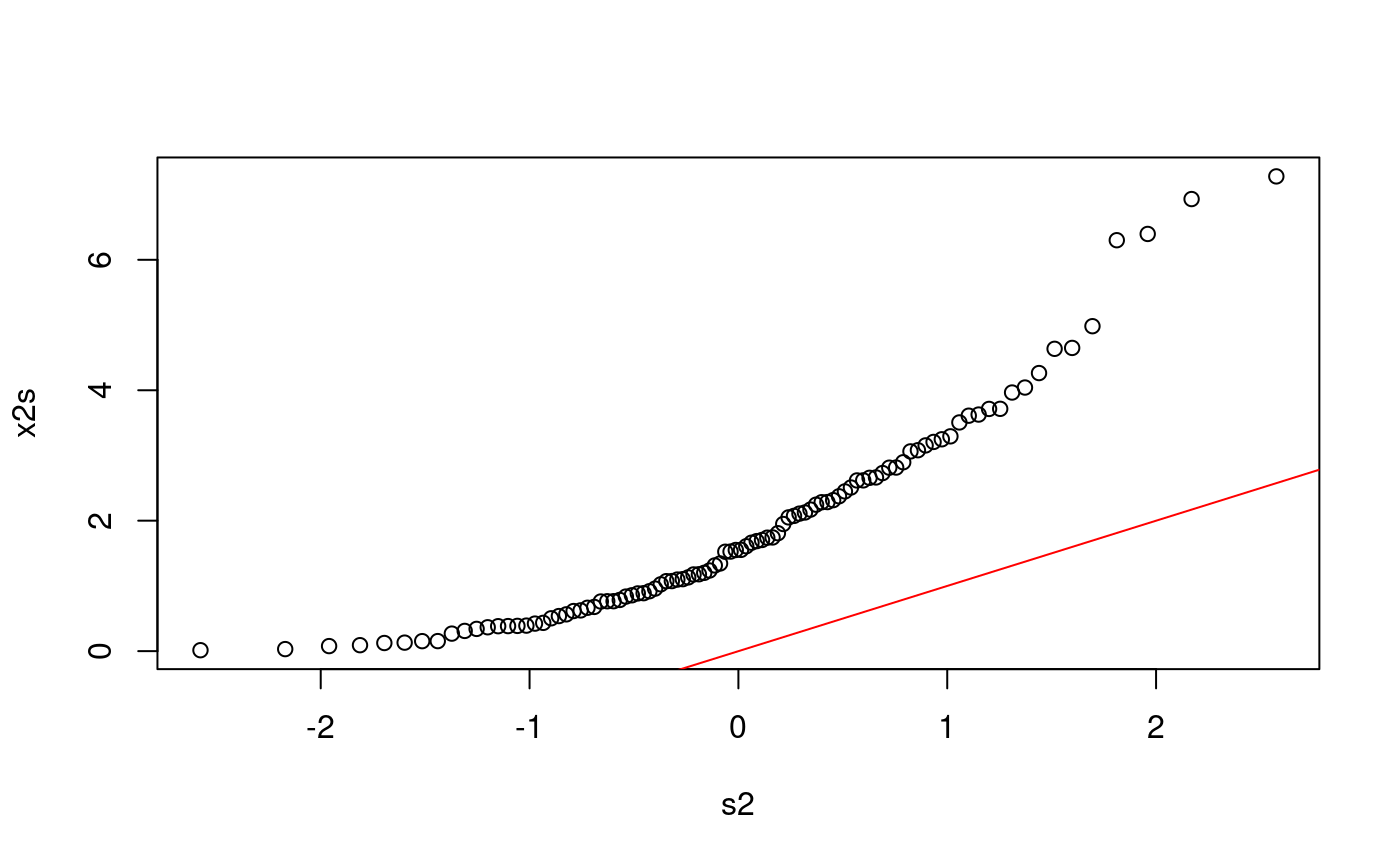
Does x200 come from N(0,1)?

n <- length(x200)
p <- ((1:n) - 0.5) / n
si <- qnorm(p)
x200.sorted <- sort(x200)
plot(si, x200.sorted)
abline(0, 1, col = "blue")

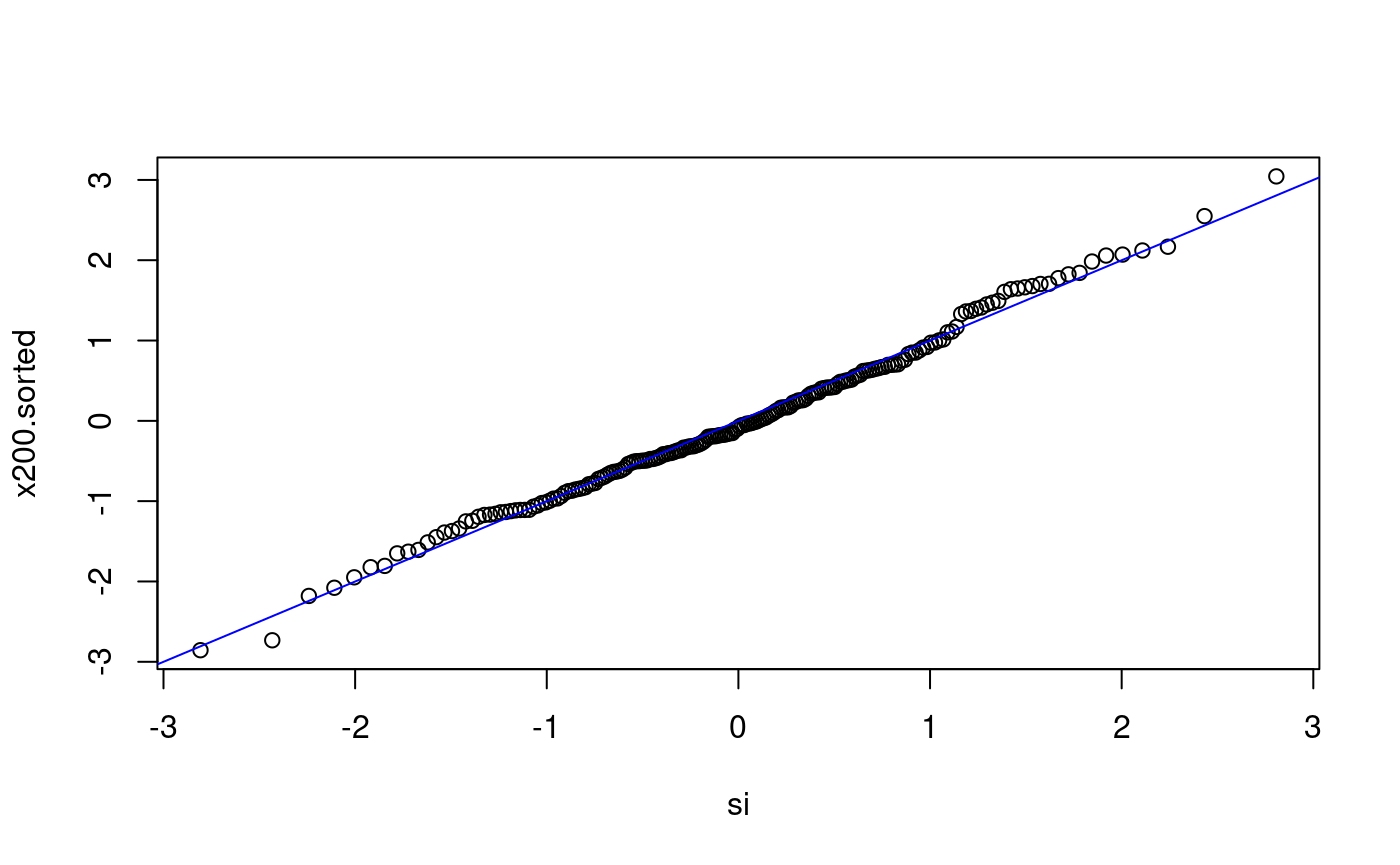
Does x200 come from Student-t with 3 d.f.?

si <- qt(p, df = 3)
plot(si, x200.sorted)
abline(0,1, col = "blue")

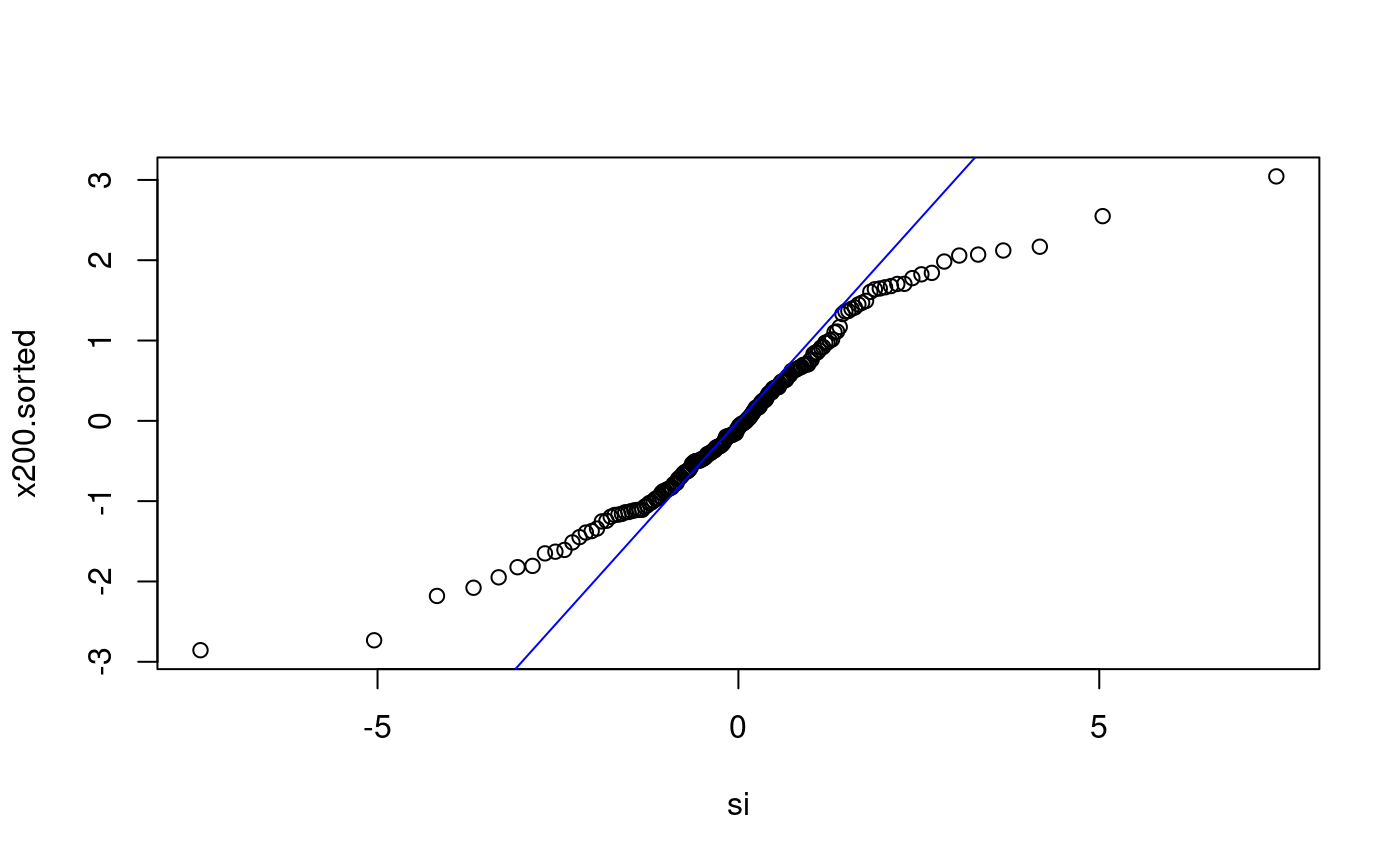
Does x500 come from N(0,1)?

n <- length(x500)                  # x500
p <- (1:n - 0.5)/n
s <- qnorm(p)
x500.sorted <- sort(x500)
plot(s, x500.sorted)
abline(0,1)                        # various ways to overlay a line
lm(x500.sorted ~ s)
## 
## Call:
## lm(formula = x500.sorted ~ s)
## 
## Coefficients:
## (Intercept)            s  
##    -0.03162      1.00690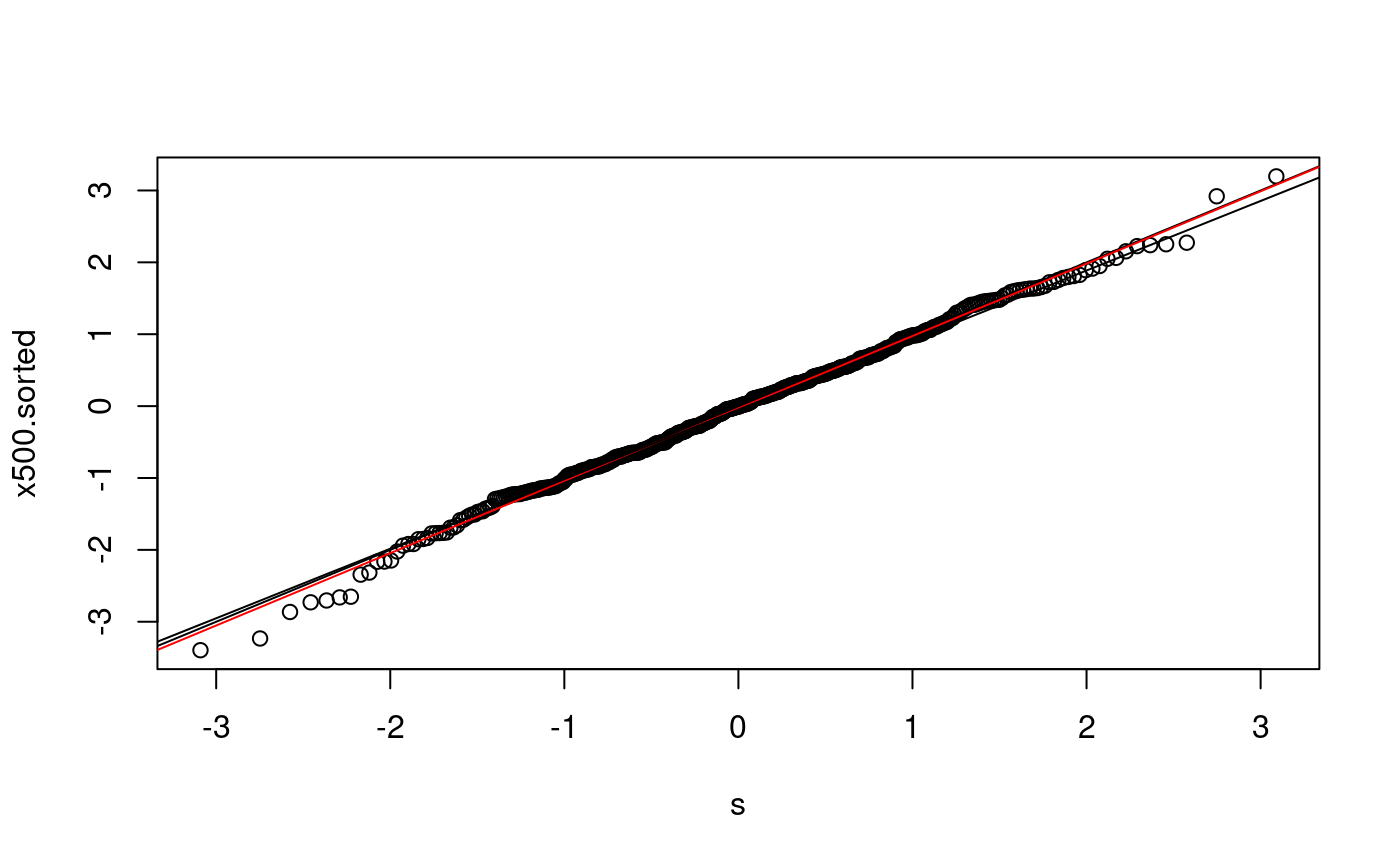
abline(lm(x500.sorted ~ s), col = "red")
qqline(x500.sorted)

qq-plots for x500 The following examples are of qq-plots for x500 with various non-matching distributions.

s <- qt(p, df = 3)      # H0 is t_3 dist
plot(s, x500.sorted)
abline(0, 1, col="blue")

s <- qnorm(p, mean = 5) # H0 is N(5,1)
plot(s,x500.sorted)
abline(0, 1, col = "blue")

s <- qnorm(p, mean = 5, sd = 2) # H0 is N(5,2^2)
plot(s, x500.sorted)
abline(0, 1, col = "blue")

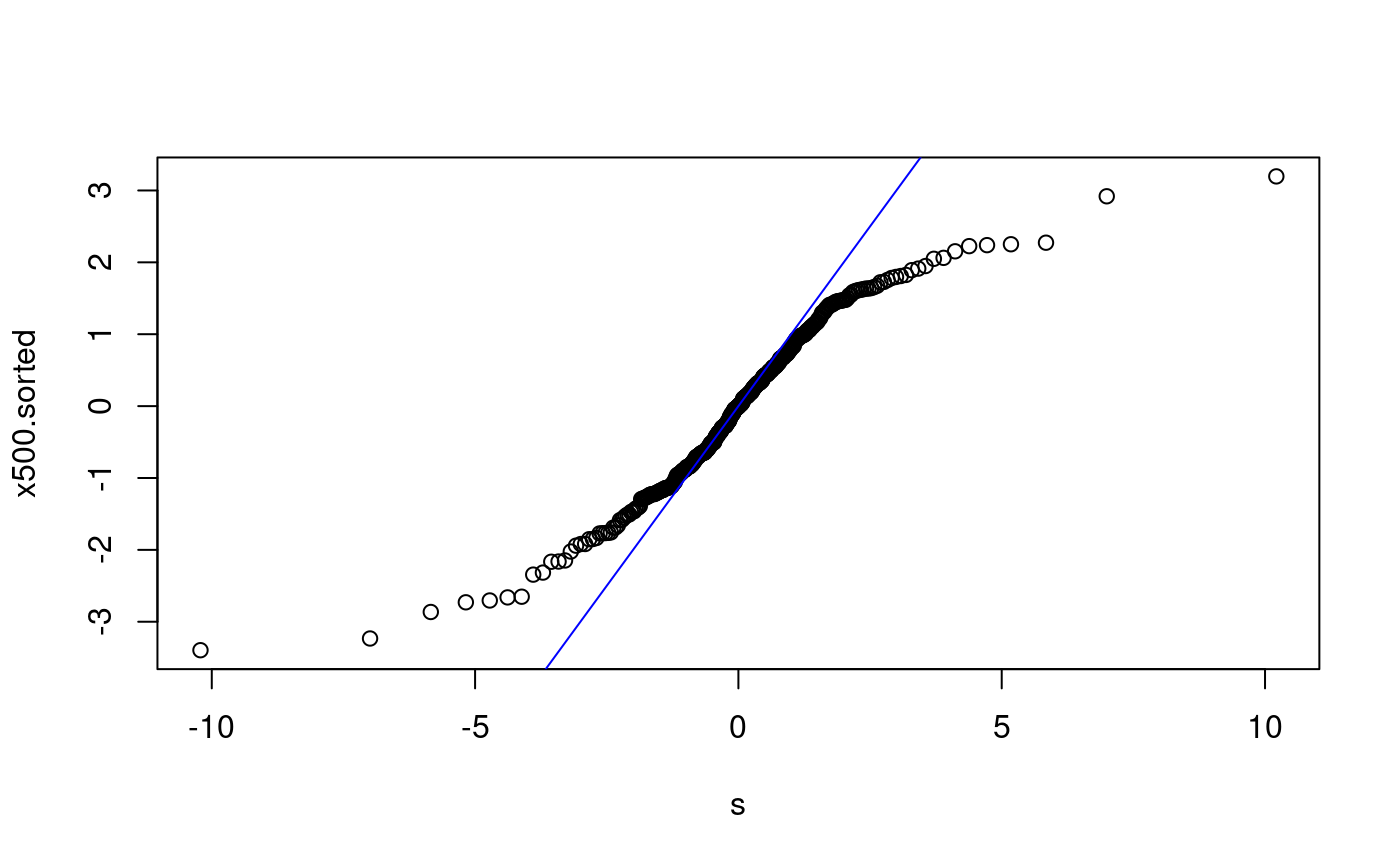
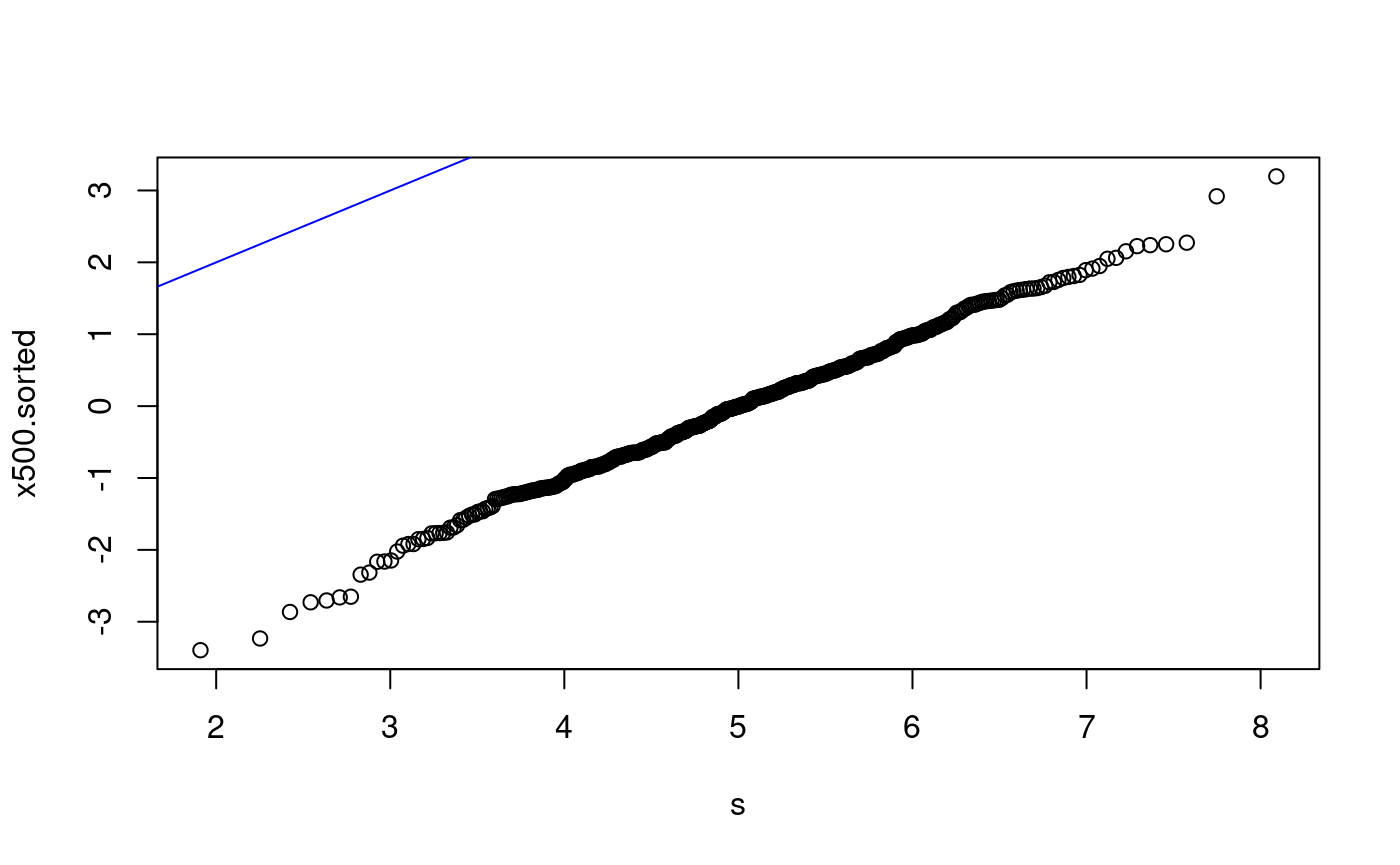
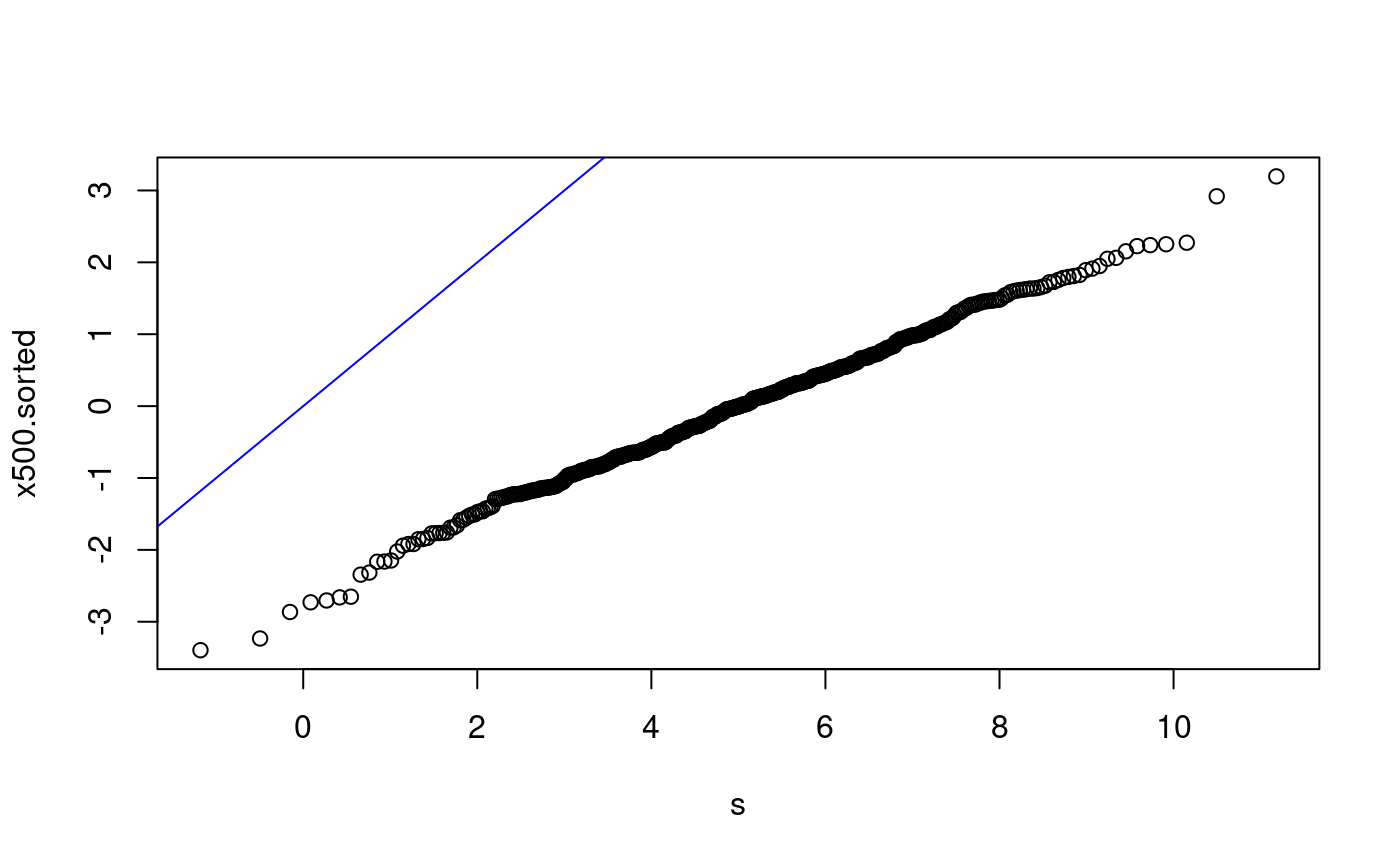
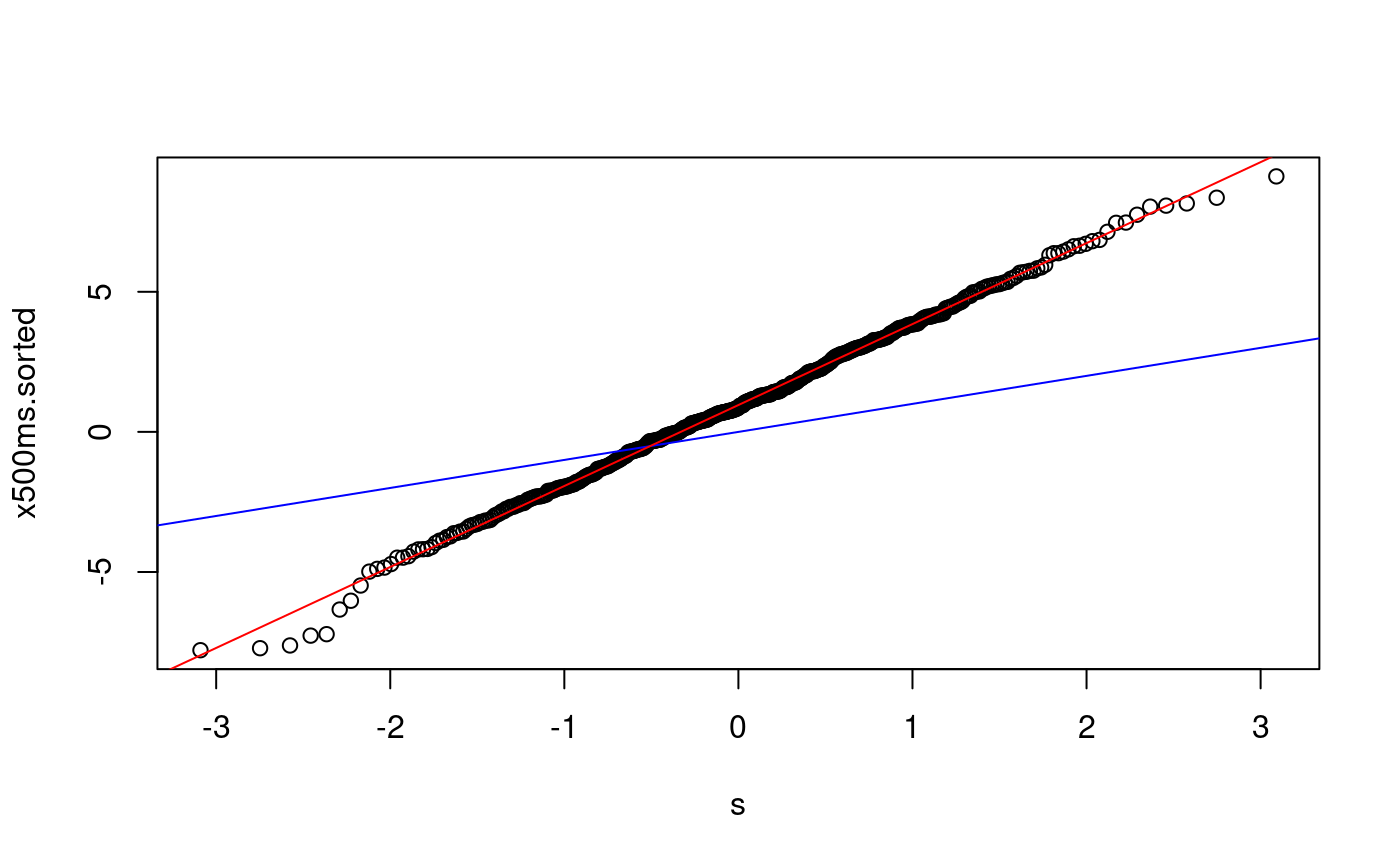
x500ms.sorted <- sort(x500ms)
p <- ((1:500) - 0.5)/500
s <- qnorm(p)
plot(s, x500ms.sorted)
abline(0, 1, col = "blue")

lmfit500 <- lm(x500ms.sorted ~ s)
summary(lmfit500)
## 
## Call:
## lm(formula = x500ms.sorted ~ s)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.34243 -0.04548  0.02041  0.07568  0.24411 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.958476   0.006293   152.3   <2e-16 ***
## s           2.889440   0.006301   458.6   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1407 on 498 degrees of freedom
## Multiple R-squared:  0.9976, Adjusted R-squared:  0.9976 
## F-statistic: 2.103e+05 on 1 and 498 DF,  p-value: < 2.2e-16
abline(lmfit500, col = "red")

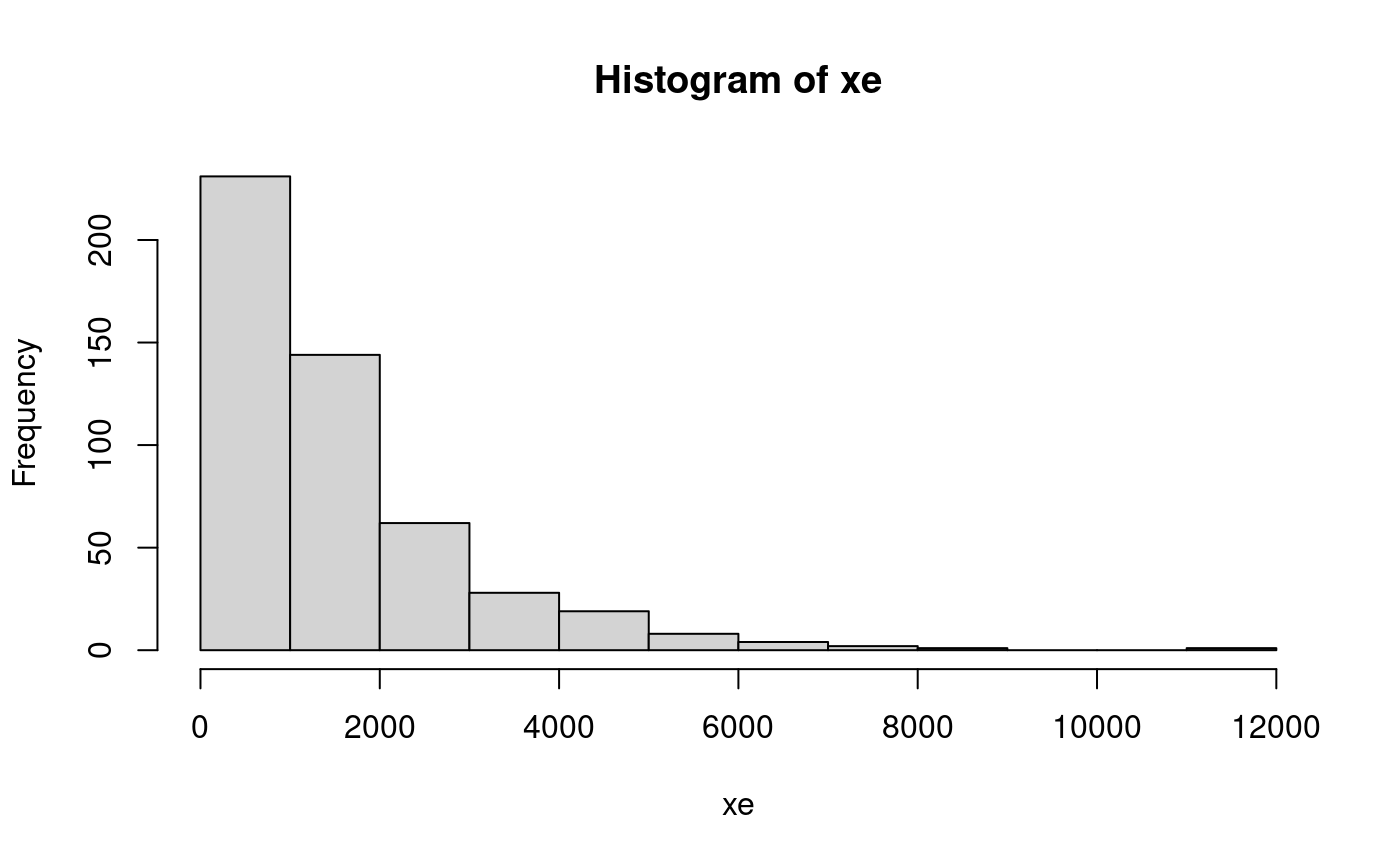
qq-plot example with an exponential distribution. First generate some data to work with: xe might represent lifetime of bulbs (incandescent have typical expected life equal to 1500 hours).

hist(xe)

n <- length(xe)
p <- ((1:n) - 0.5) / n
s <- qexp(p, rate = 1/1500)
plot(s, sort(xe))

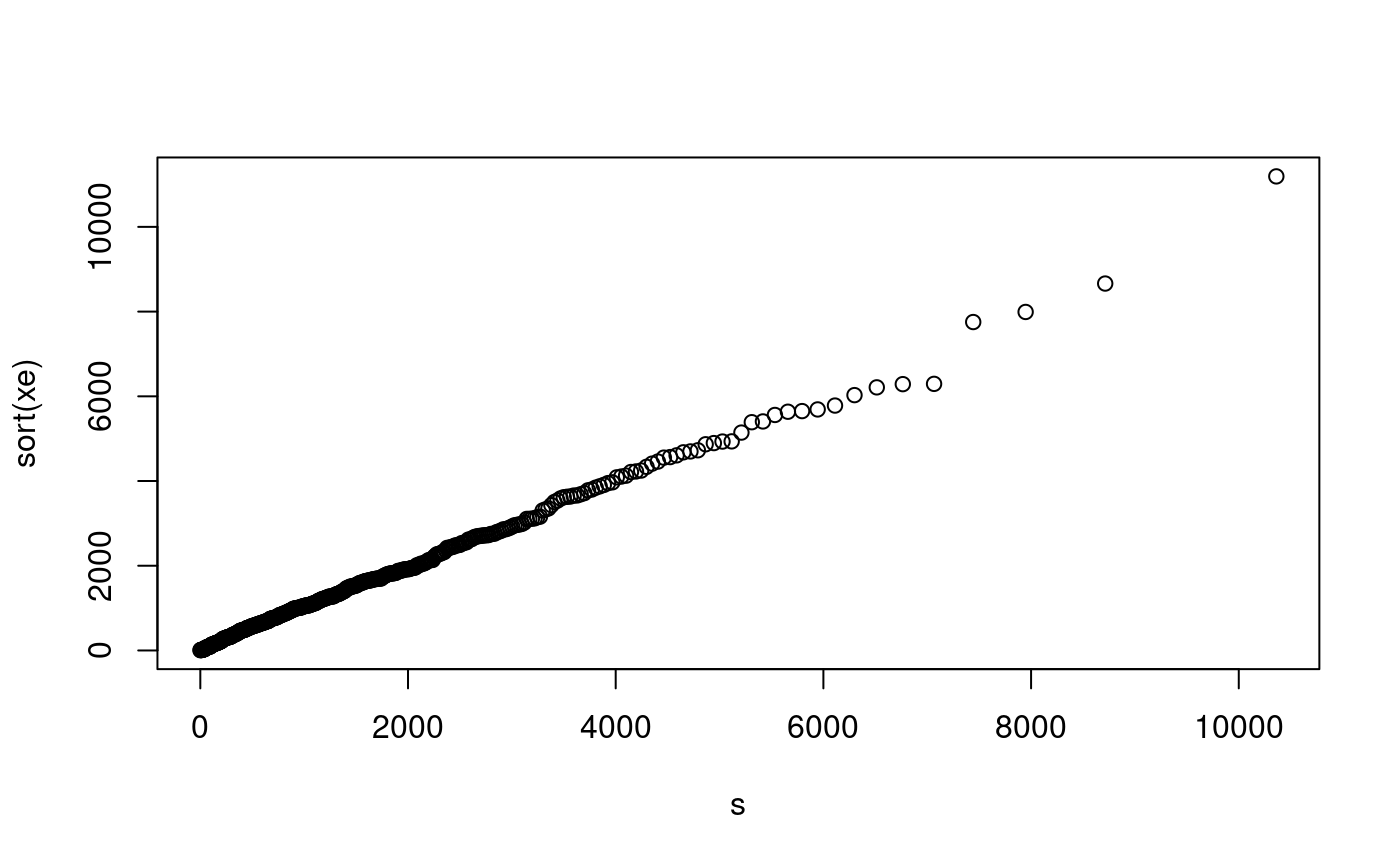
Non-diy qq-plots

qqnorm produces a normal qq-plot, i.e. a qq-plot for hypothesised normal distribution:

qqnorm(x500ms)
abline(0,1)

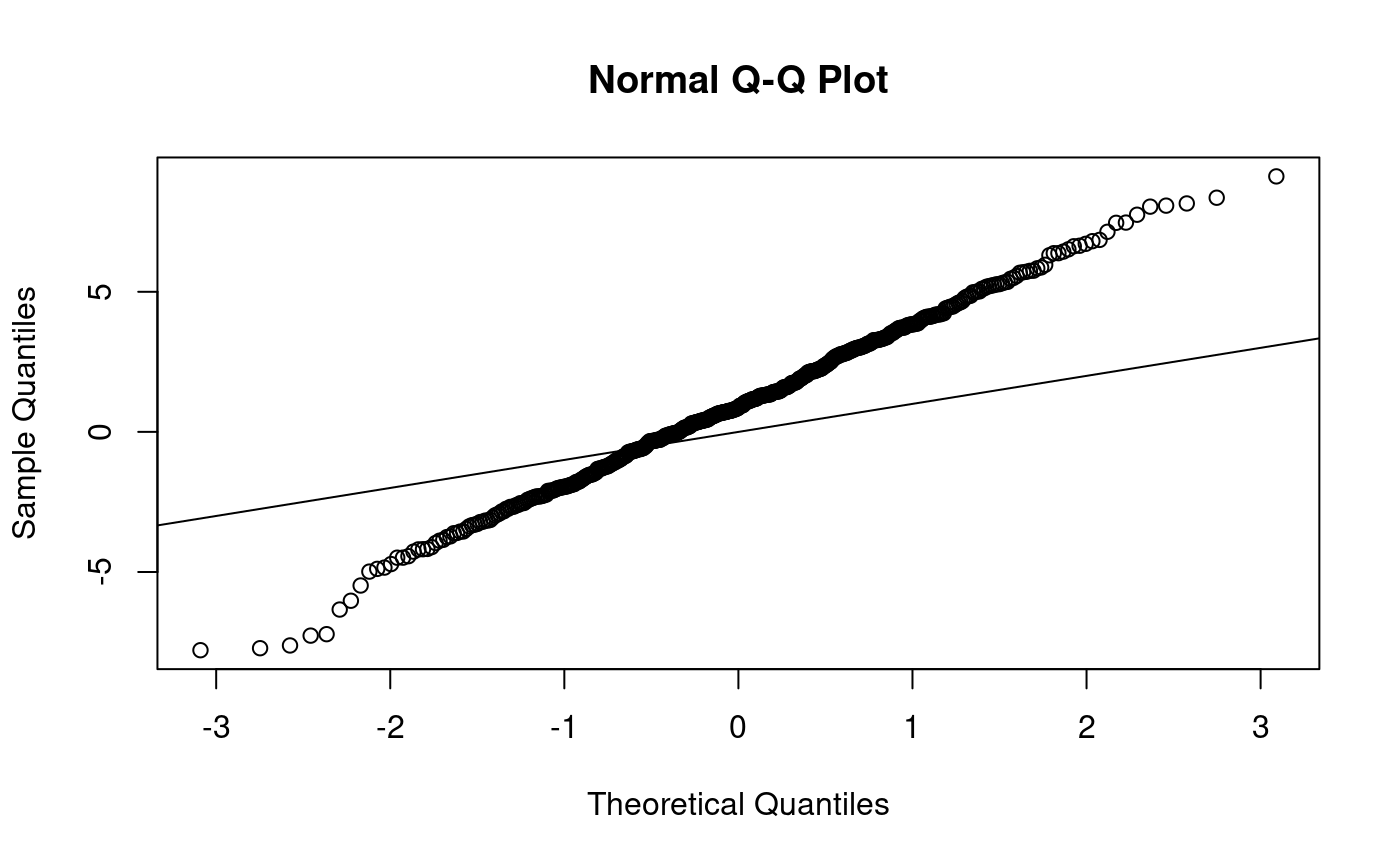
qqnorm(x500)                   # qqnorm

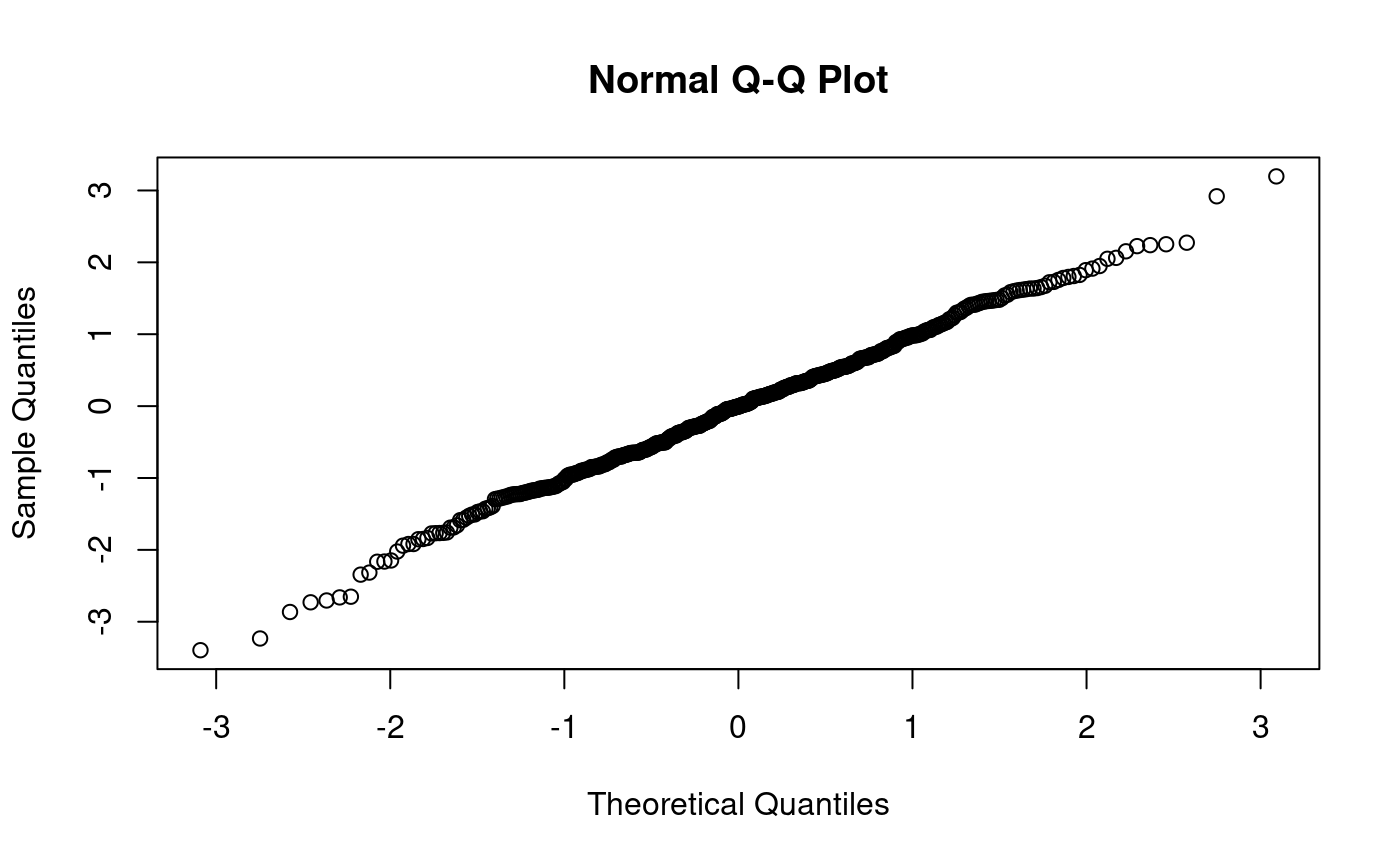
qqnorm(xe)     # no match here

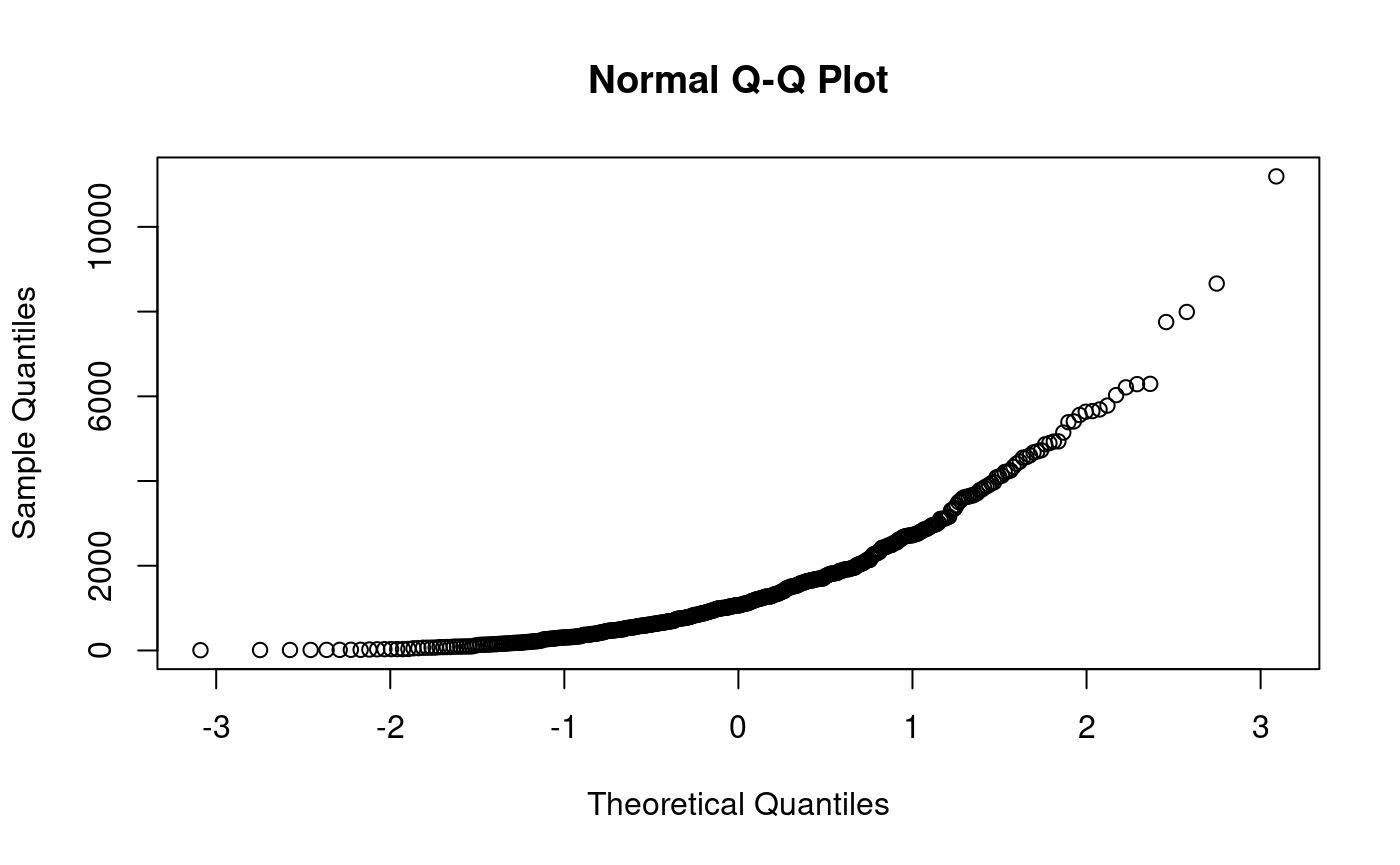
probplot() is another function for qq-plots. Without further arguments it produces a normal plot:

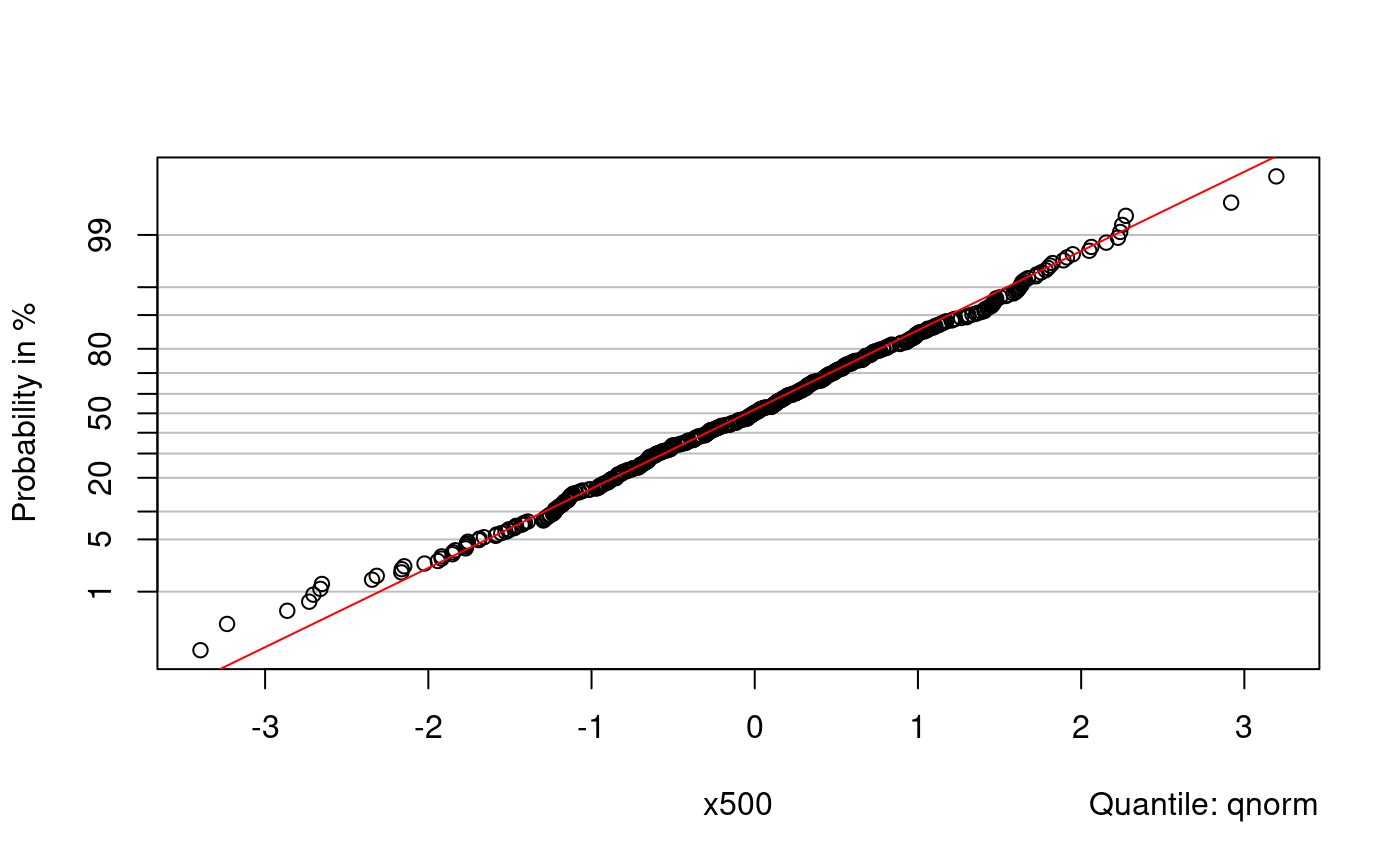
library(e1071, quiet = TRUE)  # for probplot
probplot(x500)

For other hypothesised distributions the relevant quantile function should be given. We often need to define the function ourselves.

#
# this doesn't work since probplot insists on naming the argument 'p'
# qexp1500 <- function(x) qexp(x, rate=1/1500)
#
                                        # here we oblige.

This function computes quantiles for exponential distribution with mean 1500:

qexp1500 <- function(p) qexp(p, rate = 1/1500)

(Note that probplot insists that the first argument is called ‘p’.) Compare:

qexp1500(0.5)
## [1] 1039.721
qexp(0.5, rate=1/1500)
## [1] 1039.721

Create the plot:

probplot(xe, qexp1500)

x2a <- rnorm(500, mean=5, sd=2)
qqnorm(x2a)

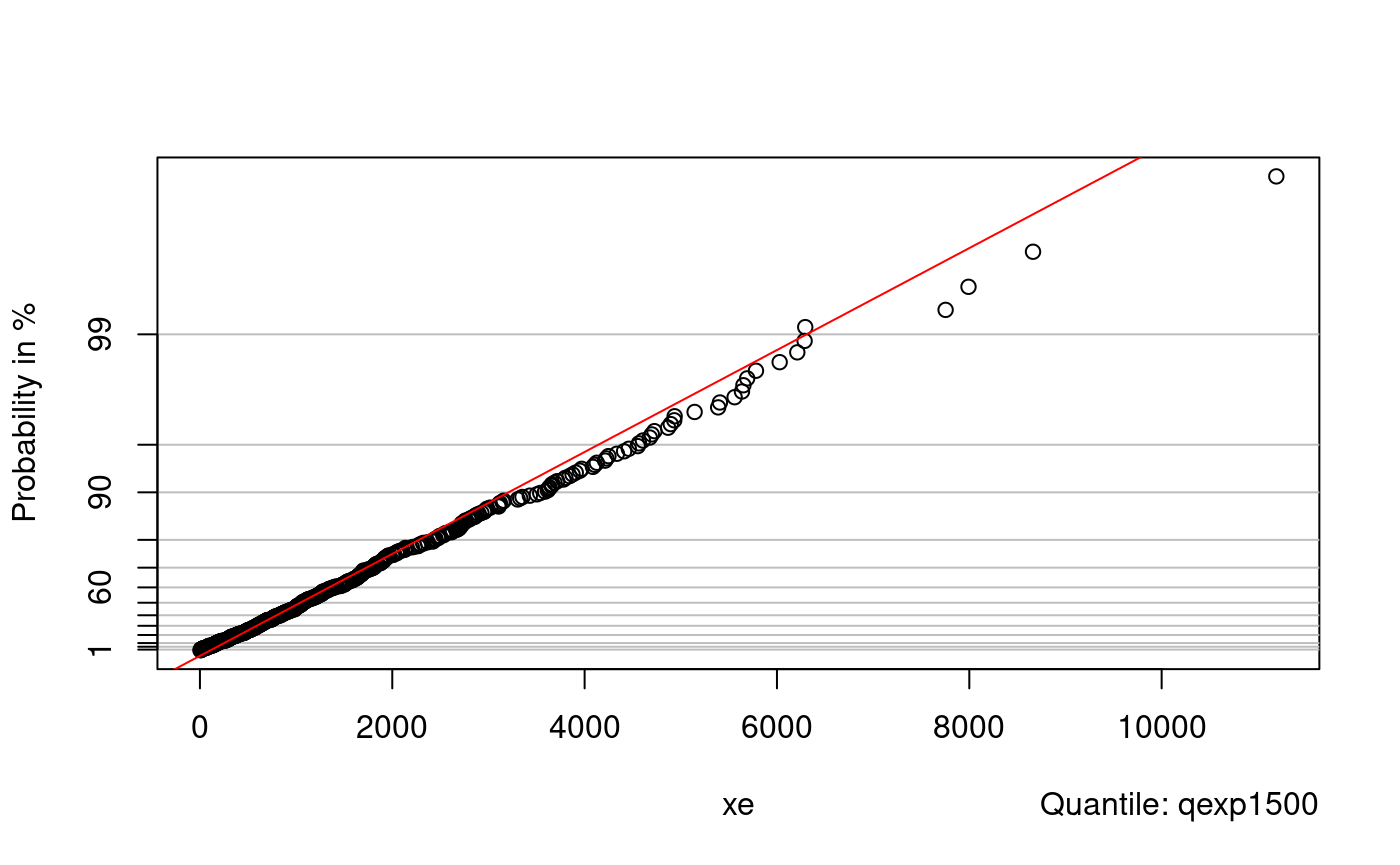
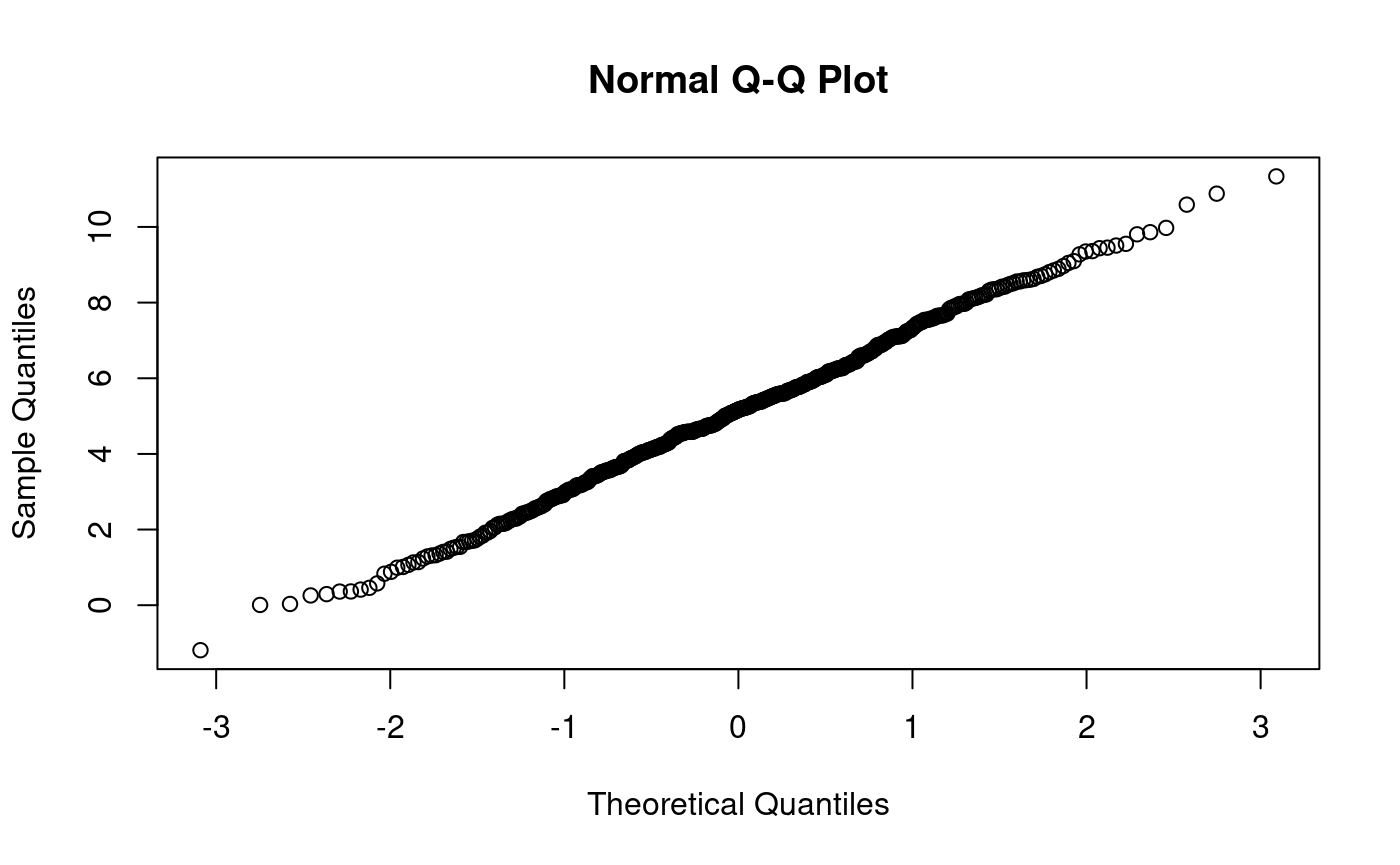
mean(x2a)
## [1] 5.11848
sd(x2a)
## [1] 2.120752

example: bulbs.txt

bulbs <- scan("bulbs.txt")
bulbs
##  [1] 1615.3880 1751.3540  951.2327 3727.3430 1333.2010  914.8320  507.4933
##  [8]  213.3106  862.1596 2217.3740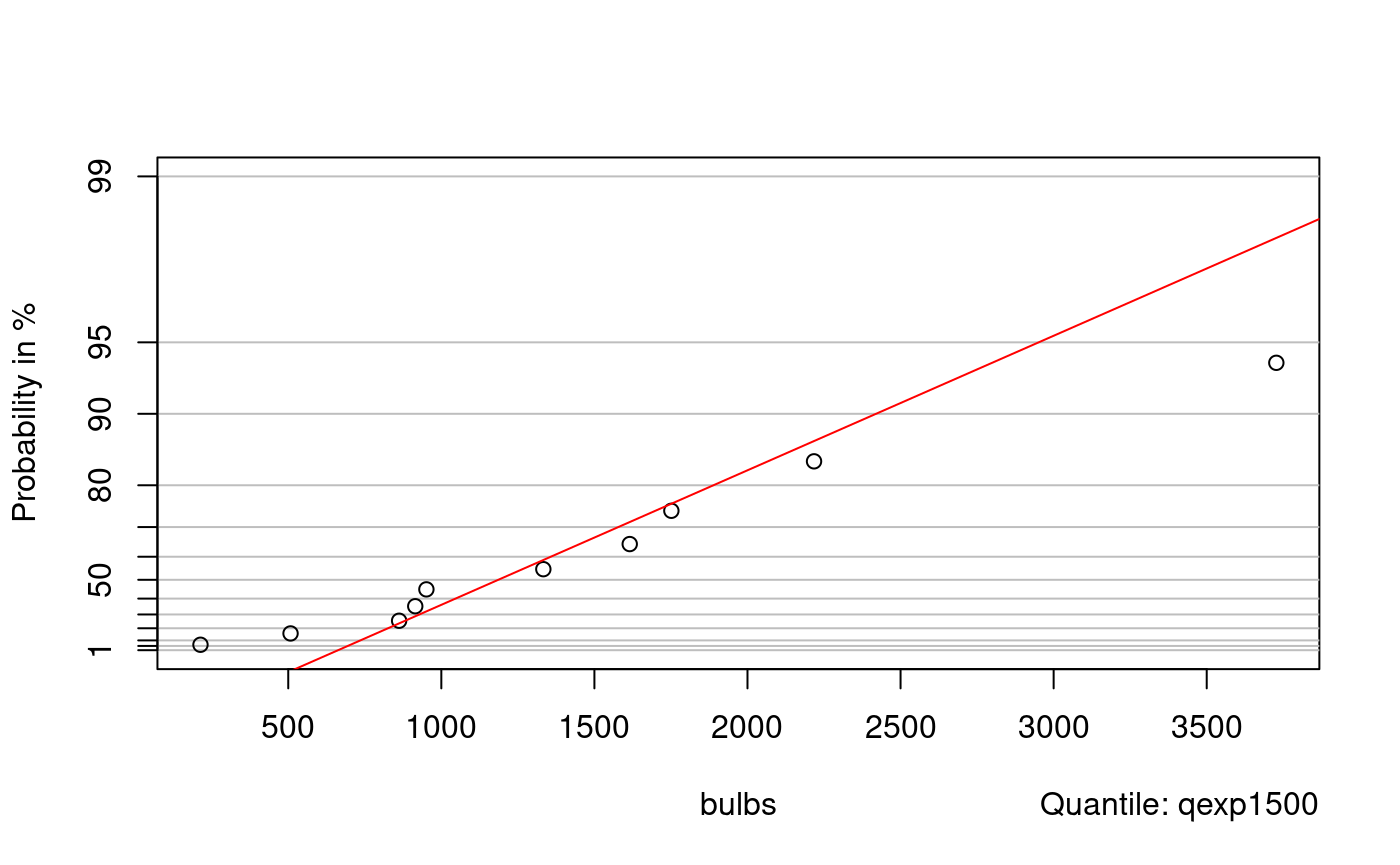
qexp1500 <- function(p){ qexp(p, rate=1/1500) }
probplot(bulbs, qdist = qexp1500)

e100 <- rexp(100, rate=1/1500)
p <- ((1:100) - 0.5)/100
s <- qexp(p, rate=1/1500)
e100s <- sort(e100)
plot(s, e100s)
abline(0,1)

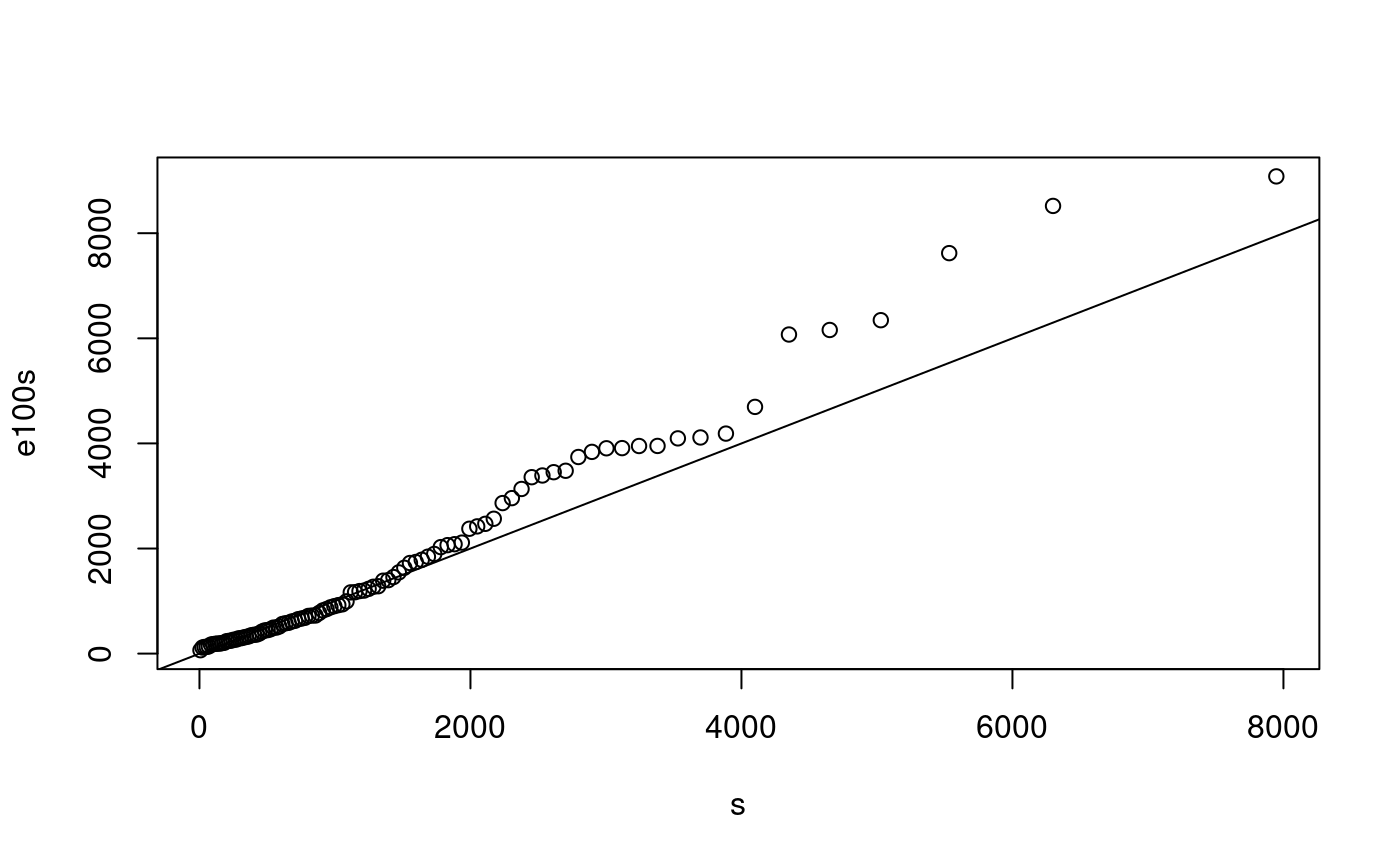
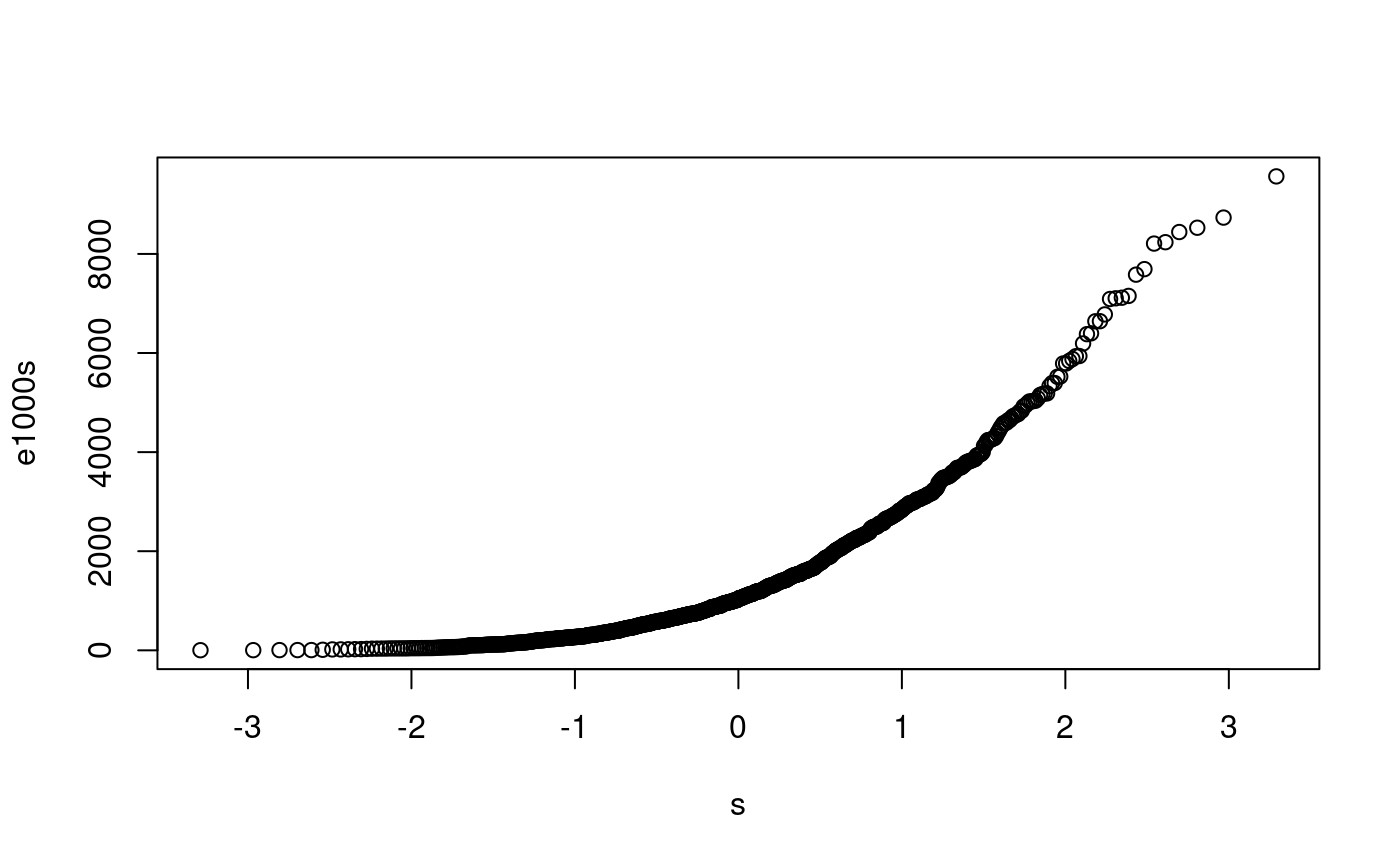
e1000 <- rexp(1000, rate=1/1500)
p <- ((1:1000) - 0.5)/1000
s <- qexp(p, rate=1/1500)
e1000s <- sort(e1000)
plot(s, e1000s)
abline(0,1)

s <- qnorm(p)
plot(s, e1000s)

library(e1071)
probplot(e1000, qexp)

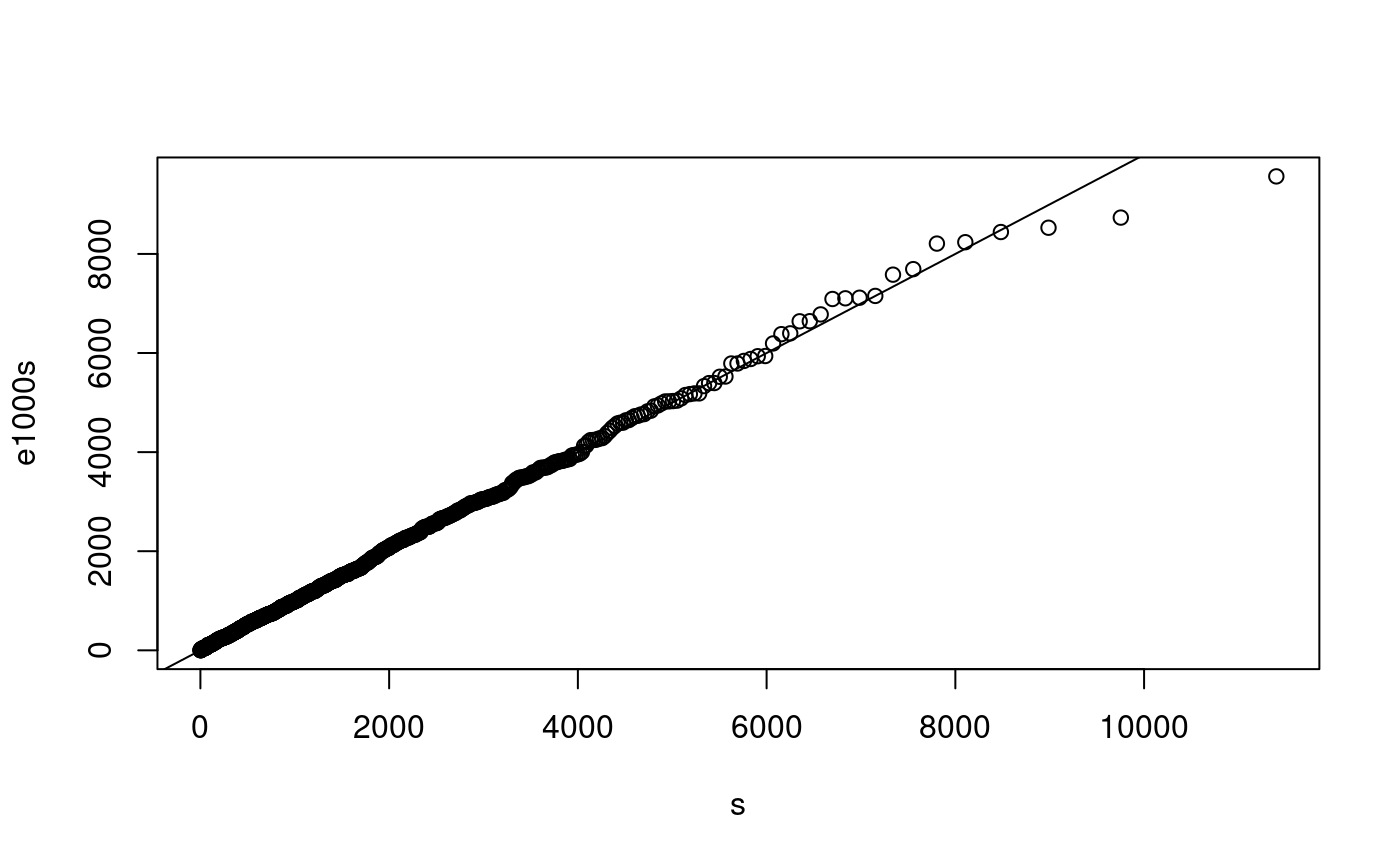
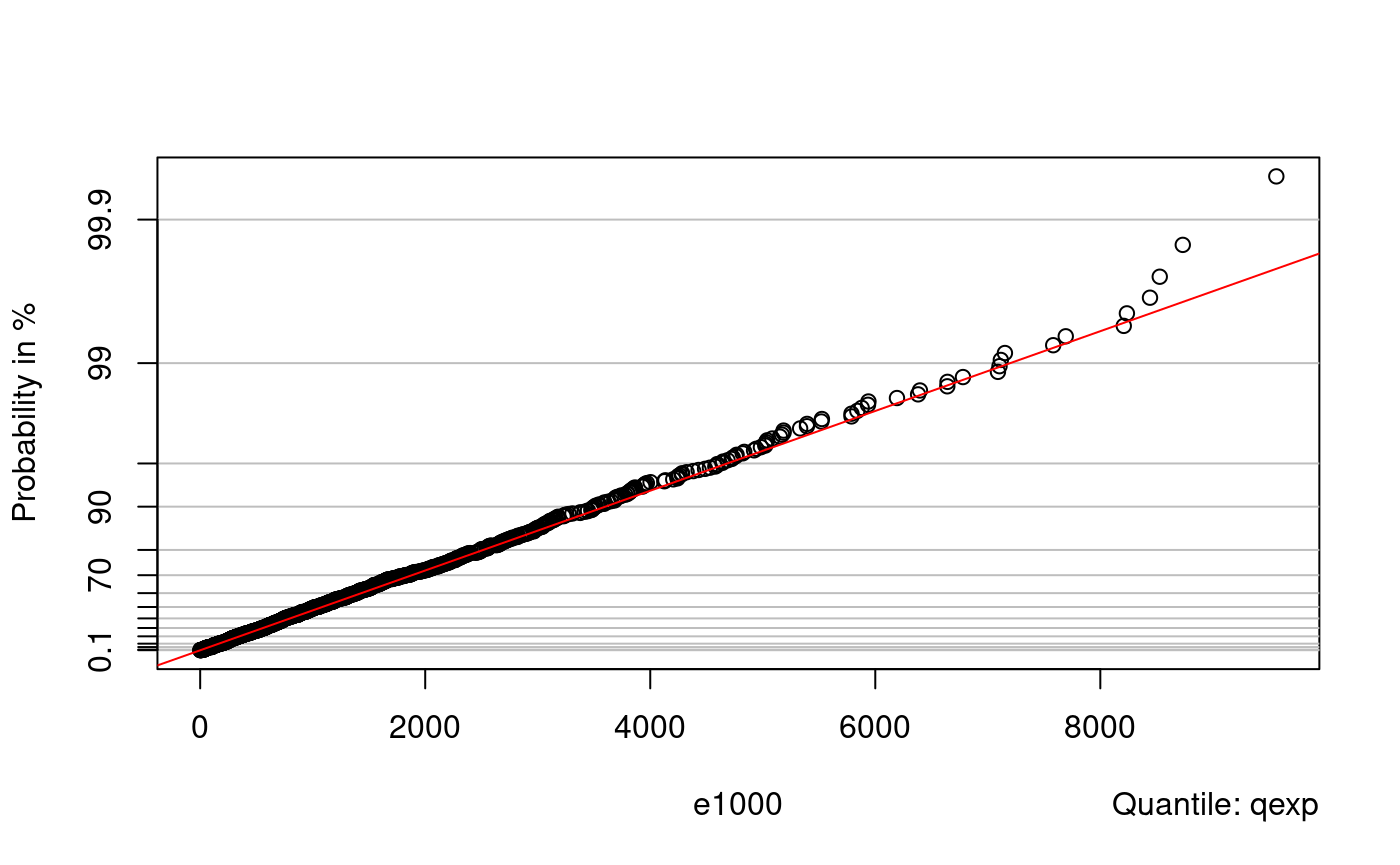
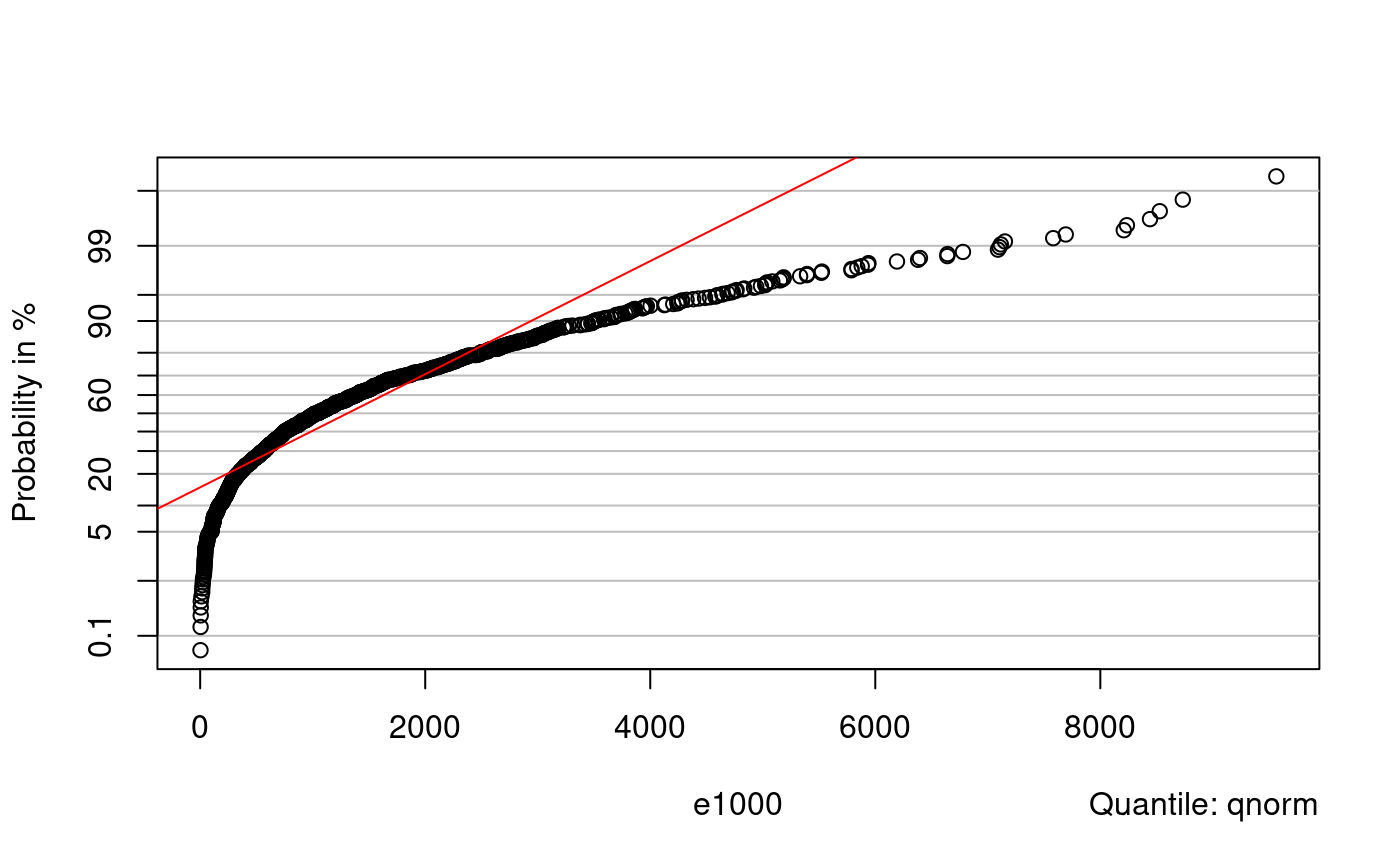
probplot(e1000, qnorm)

# ?qexp

qchisq5 <- function(p) qchisq(p, df=5)
probplot(e1000,qchisq5)

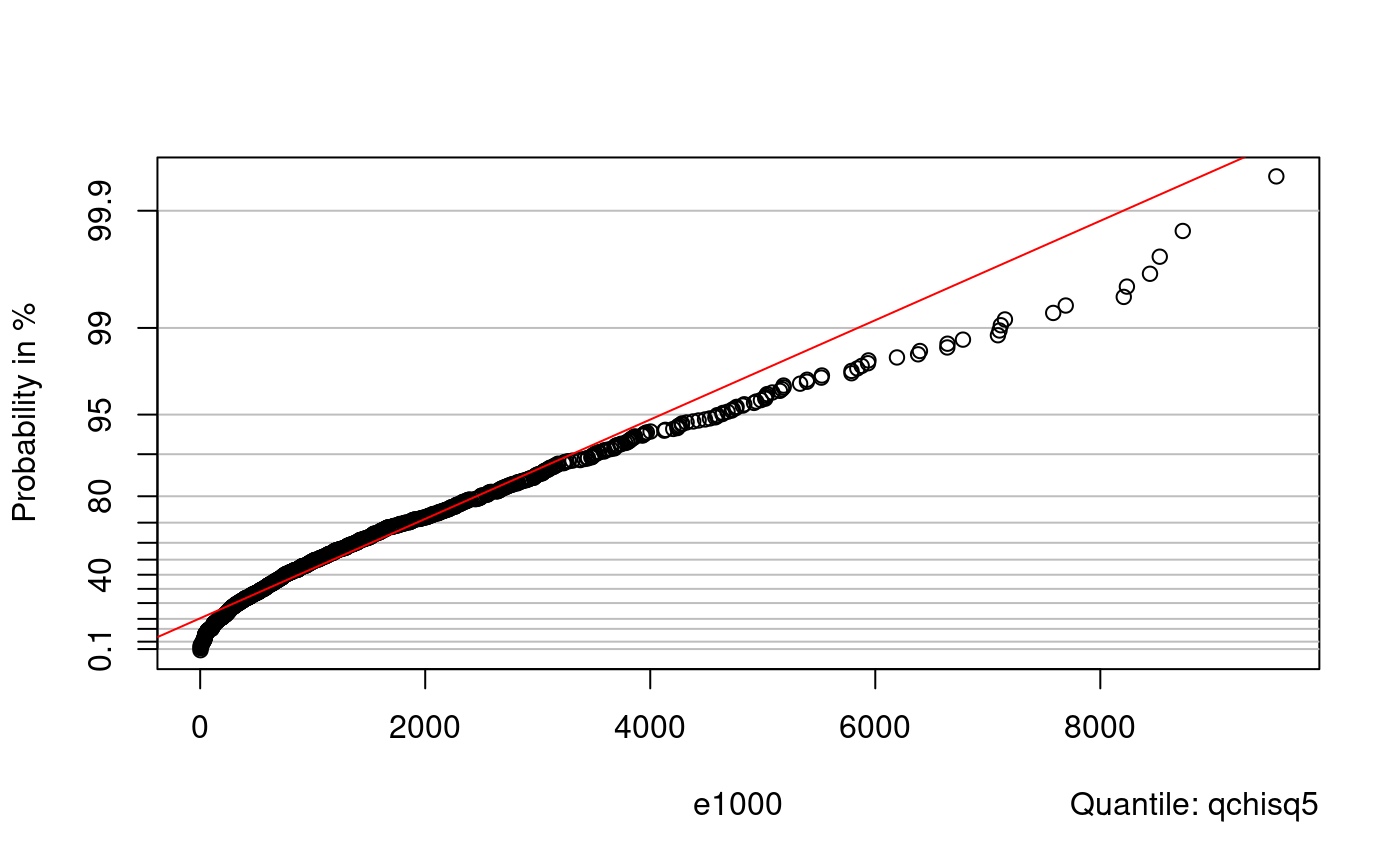
Distributions of order statistics

Approx mean and variance of order statistics example in Notes, p. 69

first using formulae on pp. 68-69

qnorm(4/(19+1))
## [1] -0.8416212
ex <- qnorm(4/(19+1))
ex
## [1] -0.8416212
exvar <- 4*(19-4+1)/((19+1)^2*(19+2))/dnorm(ex)^2
exvar
## [1] 0.09720817

… then via simulation

y <- numeric(1000)
y[1] <- sort(rnorm(19))[4]
y[2] <- sort(rnorm(19))[4]

and so on until y[1000] … :)

# ... but better use a single command
for(i in 1:1000) y[i] <- sort(rnorm(19))[4]

hist(y, freq=FALSE)  # estimate density

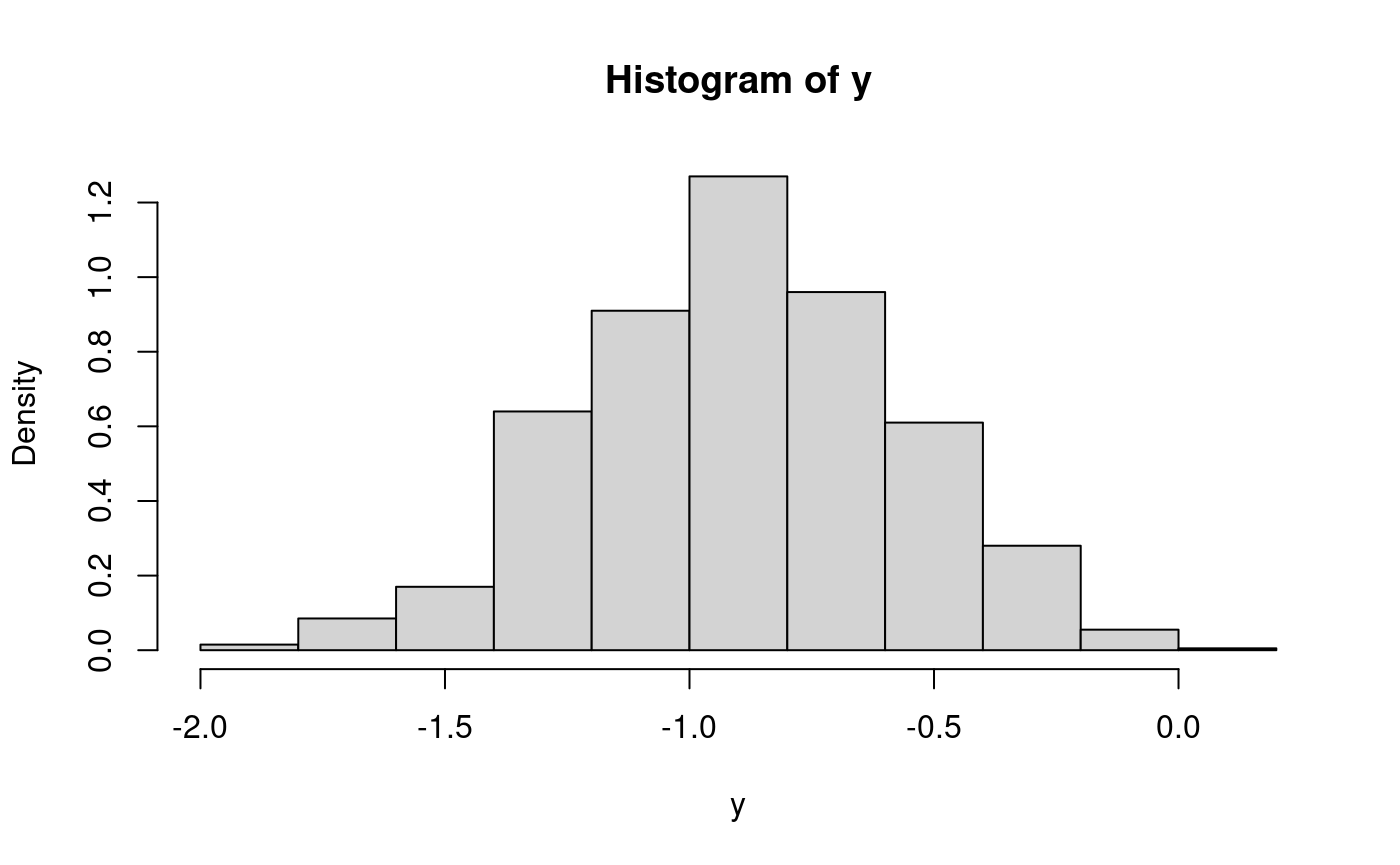
mean(y)              # estimate mean
## [1] -0.8928535
var(y)               # estimate variance
## [1] 0.1049445

this is an alternative to the ‘for’ loop (explain “replicate”)

y <- replicate(1000, sort(rnorm(19))[4])
mean(y)
## [1] -0.8994723
var(y)
## [1] 0.1124937
quantile(y, c(0.25,0.5,0.75))
##        25%        50%        75% 
## -1.1191086 -0.8994697 -0.6677008
N <- 1000
x4 <- numeric(N)
x4[1] <- sort(rnorm(19))[4]
x4[1]
## [1] -0.6385599
x4[2] <- sort(rnorm(19))[4]
# ... and so on; let's do it with a single command:
for(i in 1:N) x4[i] <- sort(rnorm(19))[4]

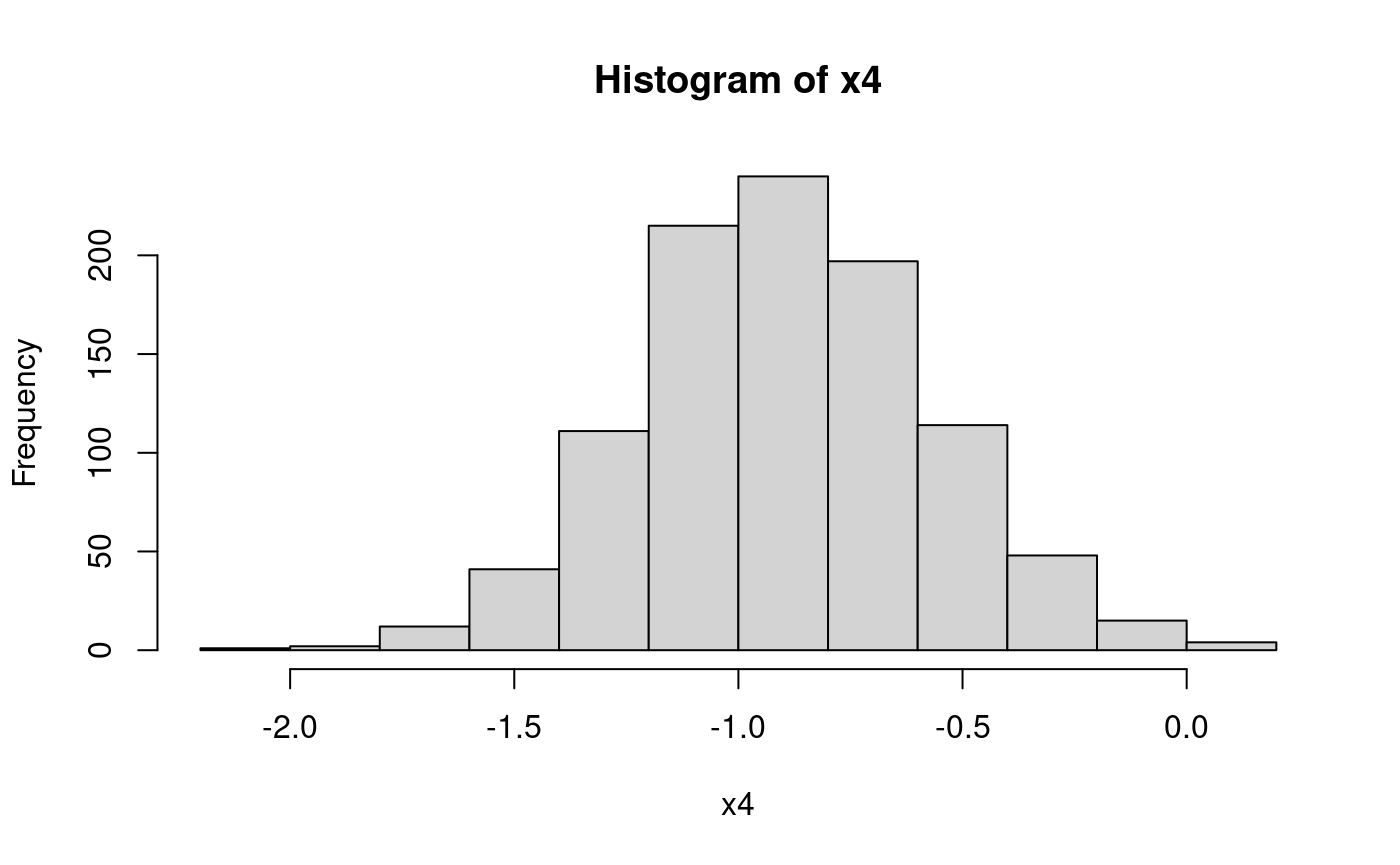
Explore the distribution of the fourth order statistic:

mean(x4)
## [1] -0.8927811
var(x4)
## [1] 0.1052386
hist(x4)

x4ecdf <- ecdf(x4)
curve(x4ecdf, from = -2, to = 2)

plot(x4ecdf)
curve(pnorm, add = TRUE, col = "red")

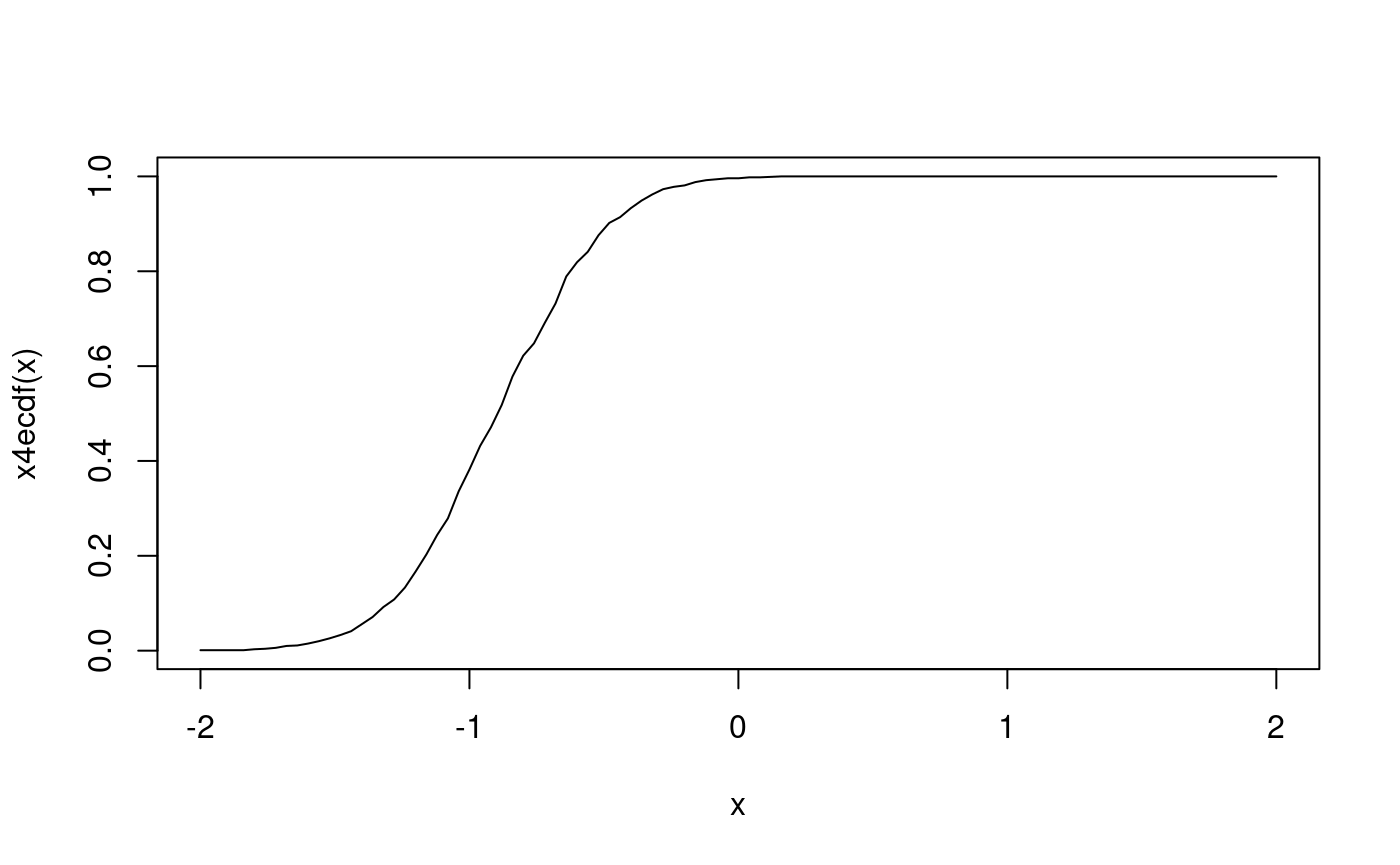
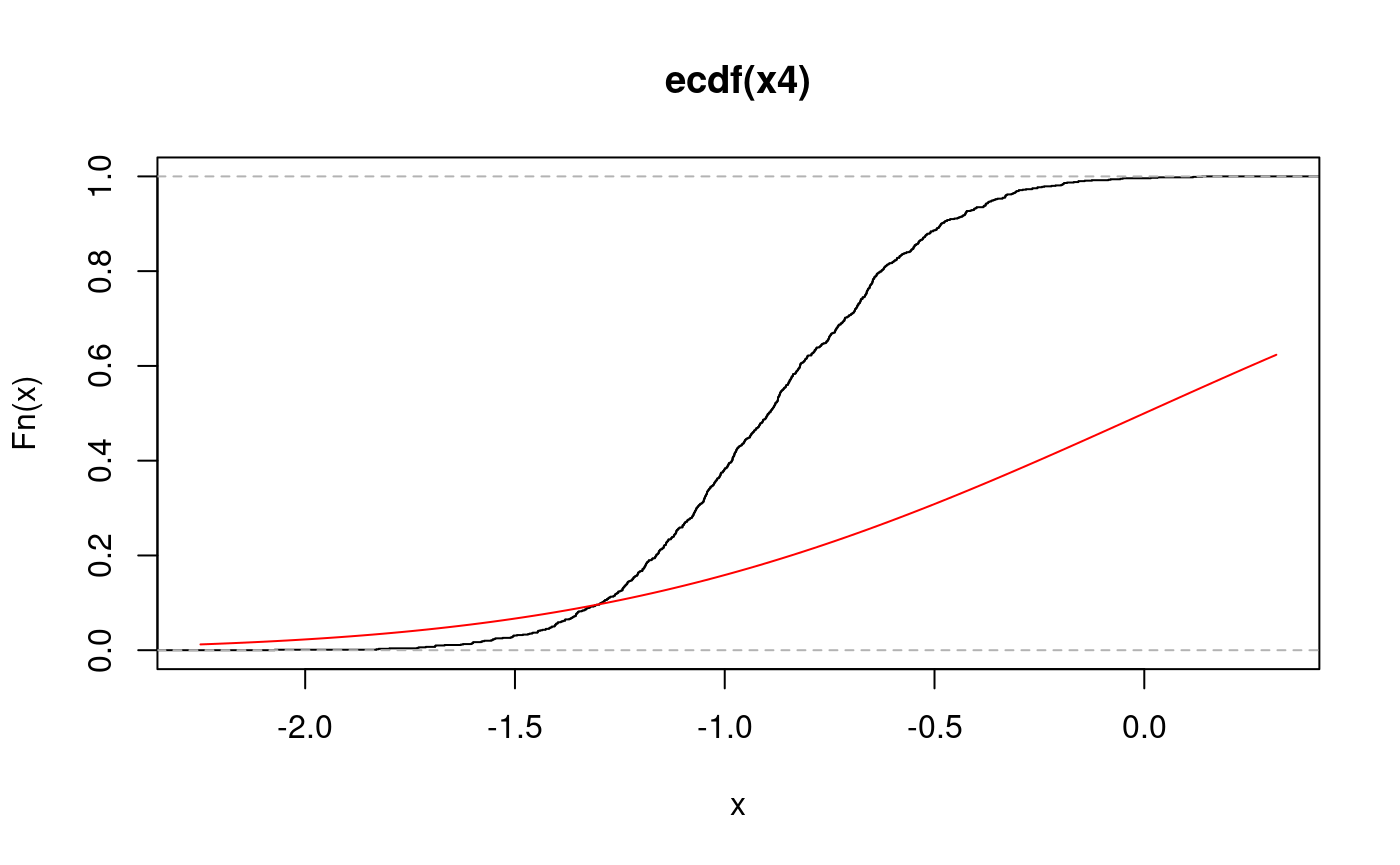
Inverse PIT

DIY generation of a random sample from distribution Expo(1/2) First generate a sample from the uniform distribution.

u <- runif(8)
u
## [1] 0.96726824 0.39173353 0.93379904 0.76794545 0.32535914 0.57392644 0.06652616
## [8] 0.87910583

Evaluate the quantiles of the required distribution (Expo(1/2) here) for the values in the U(0,1) random sample:

y <- -2*log(1-u)     #  DIY quantile function of Expo(1/2)
y
## [1] 6.8388189 0.9942844 5.4301207 2.9215656 0.7871496 1.7062866 0.1376847
## [8] 4.2256796
y1 <- qexp(u, rate = 1/2) # built-in quantile function
y1
## [1] 6.8388189 0.9942844 5.4301207 2.9215656 0.7871496 1.7062866 0.1376847
## [8] 4.2256796

The results are the same (so, qexp uses the formula -log(1-u)/lambda):

all(y == y1)
## [1] TRUE

Kolmogorov-Smirnov tests

u <- runif(100)
x <- -1/2*log(1-u)
ks.test(x, "pexp", rate=2)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  x
## D = 0.087857, p-value = 0.423
## alternative hypothesis: two-sided
ks.test(x, "pexp", rate=10)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  x
## D = 0.56113, p-value < 2.2e-16
## alternative hypothesis: two-sided
pexp2 <- function(x) pexp(x, rate = 2)
ks.test(x, pexp2)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  x
## D = 0.087857, p-value = 0.423
## alternative hypothesis: two-sided
psi.Dn(x, pexp2)
## [1] 0.08785689
x <- runif(10)
x
##  [1] 0.60772038 0.71454058 0.31063085 0.40909066 0.05476674 0.87197316
##  [7] 0.80187151 0.04541741 0.35022657 0.16252157
y <- -1/2*log(1-x)
y
##  [1] 0.46789019 0.62682769 0.18598919 0.26304634 0.02816177 1.02775768
##  [7] 0.80941975 0.02324056 0.21556577 0.08867989
y1 <- qexp(x, rate=2)
y1
##  [1] 0.46789019 0.62682769 0.18598919 0.26304634 0.02816177 1.02775768
##  [7] 0.80941975 0.02324056 0.21556577 0.08867989
all(y==y1)  # TRUE (so, qexp uses the above formula
## [1] TRUE

The cdf of the test statistic in KS test See examples for psi.pks.

# ?psi.pks
psi.pks(0.6239385,4)
## [1] 0.95
psi.pks(0.2940753,20)
## [1] 0.95
psi.pks(0.1340279,100)
## [1] 0.95
psi.pks(0.04294685,1000)
## [1] 0.95

Compare the distribution of the test statistic for various sample sizes:

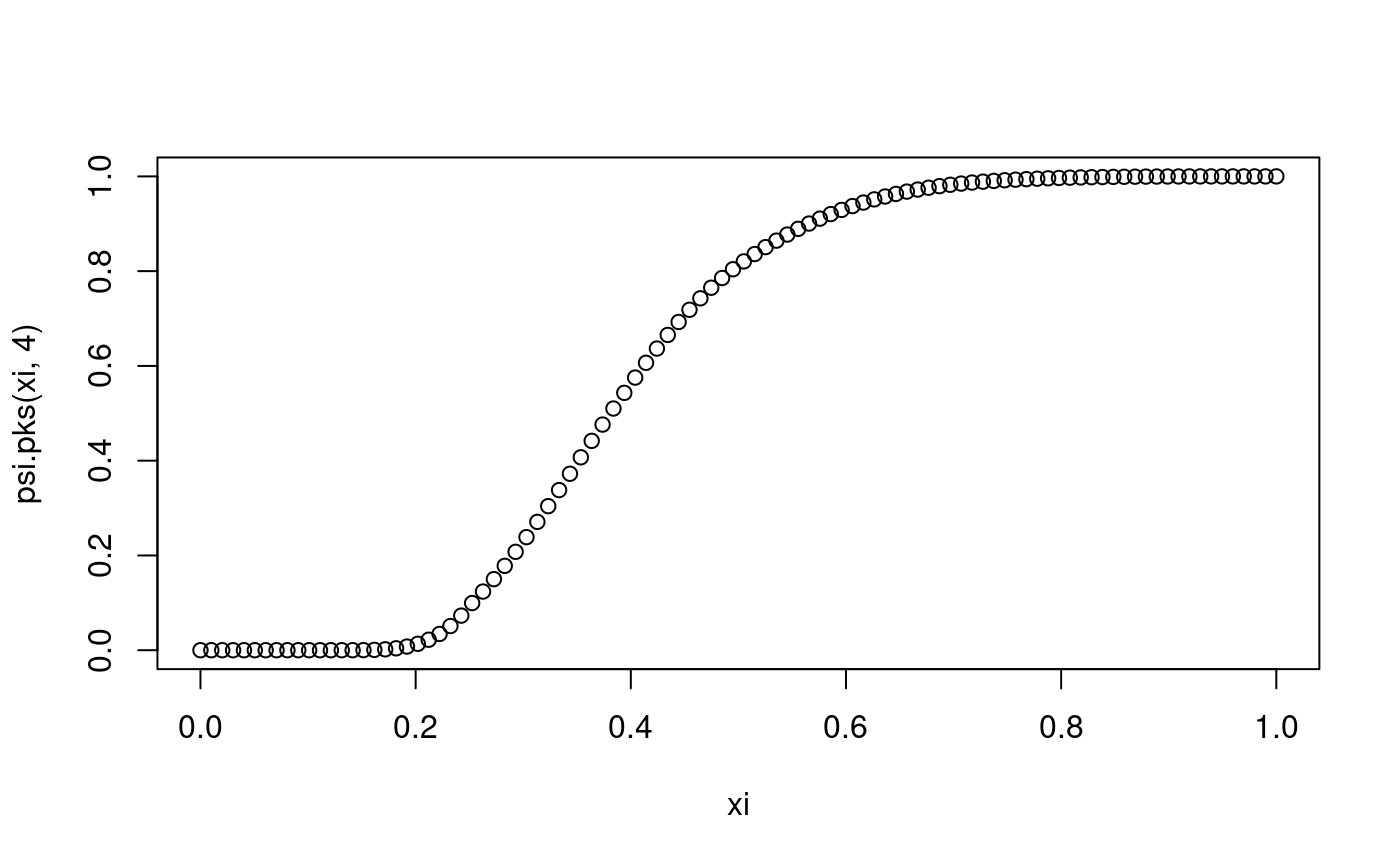
xi <- seq(0,1,length=100)            # some x values
plot(xi,psi.pks(xi,4))
lines(xi,psi.pks(xi,4))              # cdf of D_4
lines(xi,psi.pks(xi,50),col="blue")  # overlay the cdf of  D_{50}
lines(xi,psi.pks(xi,100),col="red")  # overlay the cdf of  D_{100}
abline(h=0.95, col="brown")
lines(xi,psi.pks(xi,1000),col="green")  # overlay the cdf of  D_{1000}

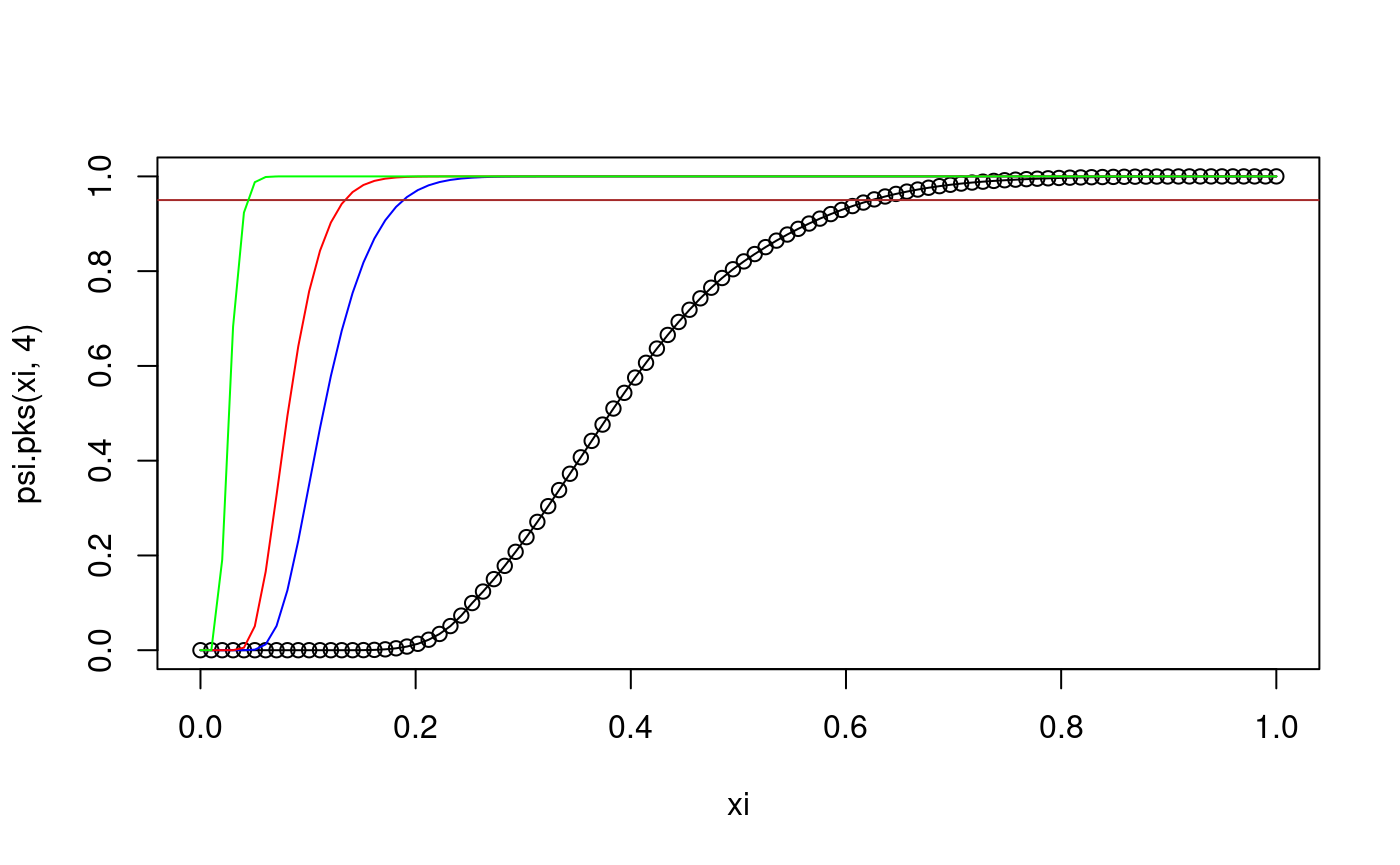
The abscissa of the intersection of the brown line with each of the curves gives the corresponding critical value of the KS test. Notice that for larger samples the critical value is smaller. In other words, smaller deviations from the hypothesised distribution function are considered significant. Similar to above using curve():

curve(psi.pks(x,4), from=0, to=1)                             # cdf of D_4
curve(psi.pks(x,10), from=0, to=1, col="blue", add=TRUE)      # cdf of D_10
curve(psi.pks(x,50), from=0, to=1, col="brown", add=TRUE)     # cdf of D_50
curve(psi.pks(x,100), from=0, to=1, col="red", add=TRUE)      # cdf of D_100
curve(psi.pks(x,1000), from=0, to=1, col="green", add=TRUE)   # cdf of D_1000
abline(h=0.95, col="brown")

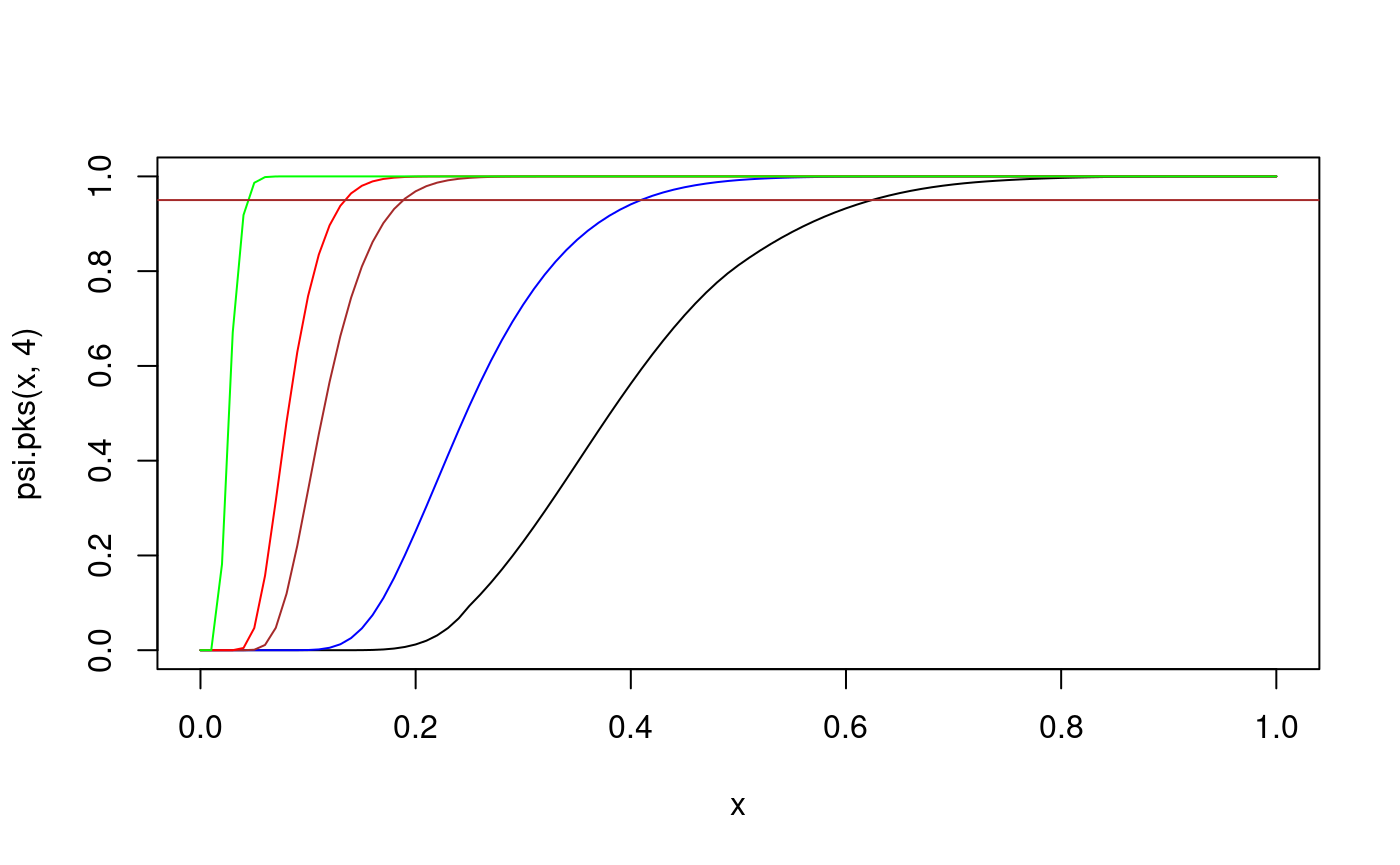
DIY Dn

x10 <- rnorm(10)

diy Dn for H_0 = cdf of N(0,1)

u10 <- pnorm(x10)
u10
##  [1] 0.50005467 0.94167283 0.57367674 0.25966462 0.79541192 0.95330771
##  [7] 0.33814719 0.06689247 0.81922995 0.23913859
u10 <- sort(pnorm(x10))
u10
##  [1] 0.06689247 0.23913859 0.25966462 0.33814719 0.50005467 0.57367674
##  [7] 0.79541192 0.81922995 0.94167283 0.95330771
n <- 10
x10Dn <- max((1:n)/n - u10, u10 - (0:(n-1)/n))
x10Dn
## [1] 0.1954119

now use psi.Dn to compute Dn, should give the same result.

psi.Dn(x10)
## [1] 0.1954119
# KS test
#
# ?psi.Dn
x
##  [1] 0.60772038 0.71454058 0.31063085 0.40909066 0.05476674 0.87197316
##  [7] 0.80187151 0.04541741 0.35022657 0.16252157
## [1] 0.5181127

The value of the statistic is the same as that from ks.test:

ks.test(x, pnorm)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  x
## D = 0.51811, p-value = 0.005074
## alternative hypothesis: two-sided
psi.Dn(x) == ks.test(x, pnorm)$statistic
##    D 
## TRUE
pe <- function(x) pexp(x, rate=1/1500)
ks.test(x, pe)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  x
## D = 0.99942, p-value < 2.2e-16
## alternative hypothesis: two-sided

KS test 2013/2014 chunk

x20
##  [1] -1.20706575  0.27742924  1.08444118 -2.34569770  0.42912469  0.50605589
##  [7] -0.57473996 -0.54663186 -0.56445200 -0.89003783 -0.47719270 -0.99838644
## [13] -0.77625389  0.06445882  0.95949406 -0.11028549 -0.51100951 -0.91119542
## [19] -0.83717168  2.41583518
x20os <- sort(x20)
pnorm(x20os, mean=3, sd=2)
##  [1] 0.003760506 0.017709607 0.022793726 0.025256282 0.025886351 0.027518385
##  [7] 0.029504455 0.036938855 0.037356192 0.038088186 0.039586504 0.041052895
## [13] 0.059956038 0.071083274 0.086711761 0.099319695 0.106203872 0.153804251
## [19] 0.169087002 0.385111807
pnorm(x20os, mean=3, sd=2) - (0:(20-1))/n
##  [1]  0.003760506 -0.082290393 -0.177206274 -0.274743718 -0.374113649
##  [6] -0.472481615 -0.570495545 -0.663061145 -0.762643808 -0.861911814
## [11] -0.960413496 -1.058947105 -1.140043962 -1.228916726 -1.313288239
## [16] -1.400680305 -1.493796128 -1.546195749 -1.630912998 -1.514888193
wrk1 <- pnorm(x20os, mean=3, sd=2) - (0:(20-1))/20
wrk2 <- (1:20)/20 - pnorm(x20os, mean=3, sd=2)
max(wrk1,wrk2)
## [1] 0.780913
Dn.x20 <- max(wrk1,wrk2)
Dn.x20
## [1] 0.780913
psi.Dn(x20)
## [1] 0.2833875
# ?psi.Dn
psi.Dn(x20, cdf=pnorm, mean=3, sd=2)
## [1] 0.780913
ks.test(x20, pnorm, mean=3, sd=2)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  x20
## D = 0.78091, p-value = 2.034e-13
## alternative hypothesis: two-sided
# ?psi.pks
psi.pks(0.5, n=20)
## [1] 0.9999621

Example migraine

#
# file.show("migraine.txt")
datamig <- scan("migraine.txt")
datamig
##  [1]  98  90 155  86  80  84  70 128  93  40 108  90 130  48  55 106 145 126 100
## [20] 115  75  95  38  66  63  32 105 118  21 142
##  [1]  98  90 155  86  80  84  70 128  93  40 108  90 130  48  55 106 145
## [18] 126 100 115  75  95  38  66  63  32 105 118  21 142

ks.test(datamig, pnorm, mean=90, sd=35)
## Warning in ks.test(datamig, pnorm, mean = 90, sd = 35): ties should not be
## present for the Kolmogorov-Smirnov test
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  datamig
## D = 0.066667, p-value = 0.9993
## alternative hypothesis: two-sided
ks.test(unique(datamig), pnorm, mean=90, sd=35)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  unique(datamig)
## D = 0.061367, p-value = 0.9996
## alternative hypothesis: two-sided
psi.Dn(unique(datamig), pnorm, mean=90, sd=35)
## [1] 0.06136731

Example from help page of psi.pks

xi <- seq(0,1,length=100)            # some x values
plot(xi, psi.pks(xi,4))               # cdf of D_4

diy Dn

x <- unique(datamig)
x
##  [1]  98  90 155  86  80  84  70 128  93  40 108 130  48  55 106 145 126 100 115
## [20]  75  95  38  66  63  32 105 118  21 142
xs <- sort(x)
xs
##  [1]  21  32  38  40  48  55  63  66  70  75  80  84  86  90  93  95  98 100 105
## [20] 106 108 115 118 126 128 130 142 145 155
n <- length(xs)
max( (1:n)/n - pnorm(xs,mean=90,sd=35), pnorm(xs,mean=90,sd=35) - (0:(n-1))/n)
## [1] 0.06136731

Dn using psi.Dn

psi.Dn(unique(datamig), pnorm, mean=90, sd=35)
## [1] 0.06136731
ks.test(unique(datamig),pnorm, mean=90, sd=35)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  unique(datamig)
## D = 0.061367, p-value = 0.9996
## alternative hypothesis: two-sided
migDn <- max( (1:n)/n - pnorm(xs,mean=90,sd=35), pnorm(xs,mean=90,sd=35) - (0:(n-1))/n)
migDn
## [1] 0.06136731
psi.pks(migDn, n)
## [1] 0.0004026694
1 - psi.pks(migDn, n)
## [1] 0.9995973

Lilliefors test for normality

apropos("psi.")
?psi.pkls.exp
?psi.plks.exp
?psi.qlks.exp

This package provides lillie.test():

library(nortest)
# ?lillie.test
lillie.test(x20)
## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  x20
## D = 0.1884, p-value = 0.06101

Further examples

Example: moths

# file.show("mothsontrees.txt")
datamoths <- scan("mothsontrees.txt")
datamoths
##  [1]  1.4  2.6  3.3  4.2  4.7  5.6  6.4  7.7  9.3 10.6 11.5 12.4 18.6 22.3
# ?punif
ks.test(datamoths, punif, min=0, max=25)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  datamoths
## D = 0.36114, p-value = 0.03843
## alternative hypothesis: two-sided

Alternatively:

mycdf <- function(q) punif(q, min=0, max=25)
ks.test(datamoths, mycdf)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  datamoths
## D = 0.36114, p-value = 0.03843
## alternative hypothesis: two-sided
mothssorted <- sort(datamoths)

val <- punif(mothssorted, min=0, max=25)
length(datamoths)
## [1] 14
n <- 14
(1:n)/n
##  [1] 0.07142857 0.14285714 0.21428571 0.28571429 0.35714286 0.42857143
##  [7] 0.50000000 0.57142857 0.64285714 0.71428571 0.78571429 0.85714286
## [13] 0.92857143 1.00000000
(1:n)/n - val
##  [1] 0.01542857 0.03885714 0.08228571 0.11771429 0.16914286 0.20457143
##  [7] 0.24400000 0.26342857 0.27085714 0.29028571 0.32571429 0.36114286
## [13] 0.18457143 0.10800000
val - (0:(n-1))/n
##  [1]  0.05600000  0.03257143 -0.01085714 -0.04628571 -0.09771429 -0.13314286
##  [7] -0.17257143 -0.19200000 -0.19942857 -0.21885714 -0.25428571 -0.28971429
## [13] -0.11314286 -0.03657143
max( (1:n)/n - val, val - (0:(n-1))/n )
## [1] 0.3611429
ks.test(datamoths, "punif", min=0, max=25)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  datamoths
## D = 0.36114, p-value = 0.03843
## alternative hypothesis: two-sided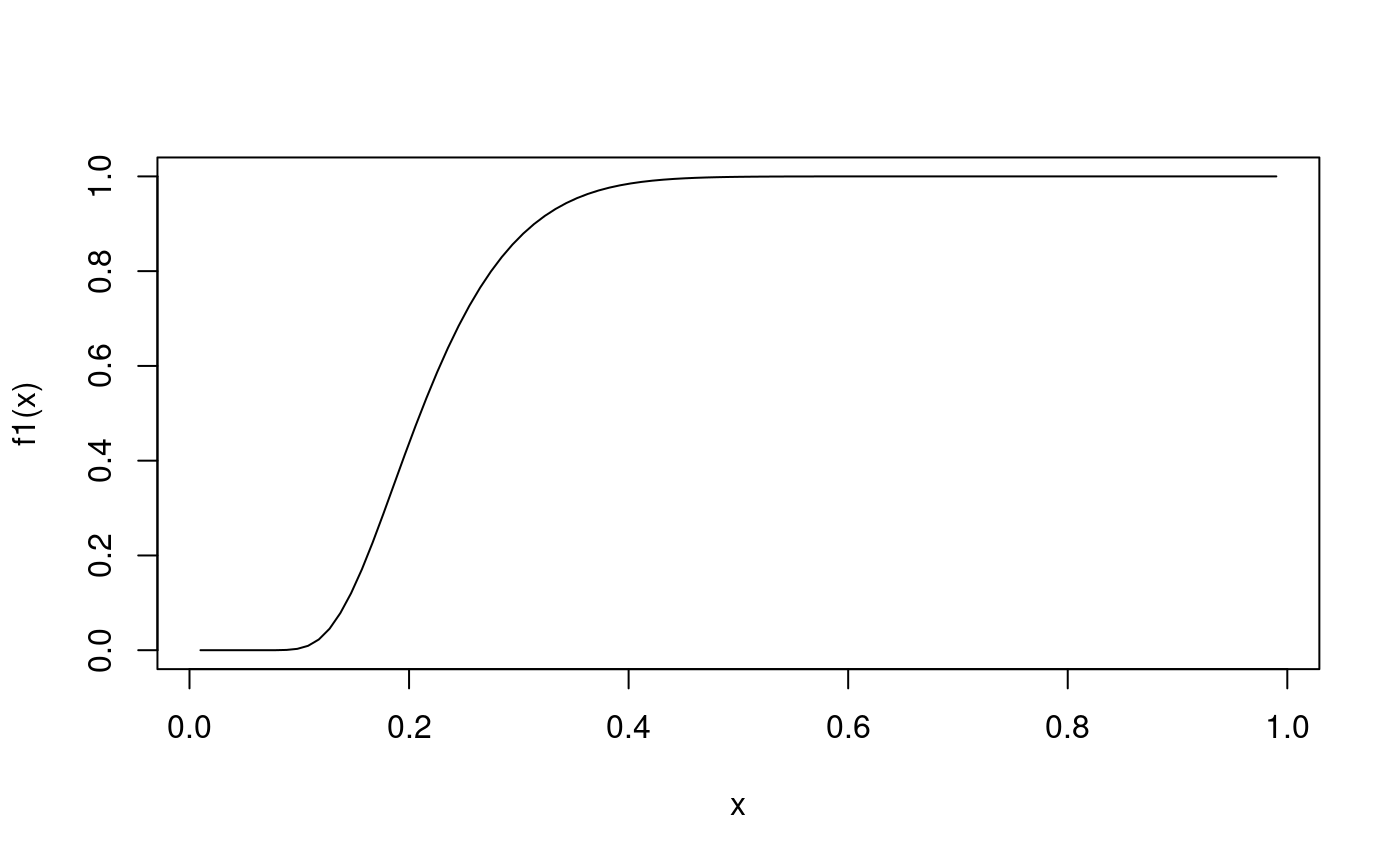
f1 <- function(x) psi.pks(x,14)
curve(f1, from=0.01, 0.99)

xi <- seq(0,1, 0.01)
head(cbind(xi, "f1(xi)" = f1(xi)))
##        xi       f1(xi)
## [1,] 0.00 0.000000e+00
## [2,] 0.01 0.000000e+00
## [3,] 0.02 0.000000e+00
## [4,] 0.03 0.000000e+00
## [5,] 0.04 1.007287e-18
## [6,] 0.05 2.105987e-11
ks.test(datamoths, "punif", min=0, max=25)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  datamoths
## D = 0.36114, p-value = 0.03843
## alternative hypothesis: two-sided
d14 <- max( (1:n)/n - val, val - (0:(n-1))/n )
d14
## [1] 0.3611429
1 - psi.pks(d14,14)
## [1] 0.03842822
ks.test(datamoths, "punif", min=0, max=25)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  datamoths
## D = 0.36114, p-value = 0.03843
## alternative hypothesis: two-sided

Example: datasales

datasales <- c(2,4,8,18,9,11,13)
ks.test(datasales, "pnorm", mean=10, sd=3)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  datasales
## D = 0.26296, p-value = 0.6278
## alternative hypothesis: two-sided

Example: barbiturate

# file.show("barbiturate.txt")
databarbi <- scan("barbiturate.txt")
databarbi
##  [1] 2.70 2.20 2.80 0.90 0.30 4.30 6.20 1.25 0.90 0.60 3.00 1.60 3.20 4.10 0.79
## [16] 3.90 0.72 1.30 7.70 2.50 1.10 6.70 1.70 3.50 5.10 1.66 2.00 3.70 1.12 0.64
## [31] 2.80 6.10
lillie.test(databarbi)
## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  databarbi
## D = 0.13552, p-value = 0.1416
ks.test(databarbi,pnorm,mean=mean(databarbi), sd=sd(databarbi))
## Warning in ks.test(databarbi, pnorm, mean = mean(databarbi), sd =
## sd(databarbi)): ties should not be present for the Kolmogorov-Smirnov test
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  databarbi
## D = 0.13552, p-value = 0.5993
## alternative hypothesis: two-sided

Example: bulbs1000

databulbs <- scan("bulbs1000.txt")
databulbs
##  [1]  730 1648 1321  319  696   21  192  780 1659  167
ks.test(databulbs, "pexp", rate=2)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  databulbs
## D = 1, p-value < 2.2e-16
## alternative hypothesis: two-sided
ks.test(databulbs, "pexp", rate=1/1000)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  databulbs
## D = 0.19033, p-value = 0.7978
## alternative hypothesis: two-sided
mean(databulbs)
## [1] 753.3
1/mean(databulbs)
## [1] 0.001327492
# apropos("psi.")
# ?psi.lks.exp.test
psi.lks.exp.test(databulbs)
## 
##  One-sample Lilliefors test for exponential distribution
## 
## data:  databulbs
## Dn.Lillie.exp = 0.20305, p-value = 0.525
## alternative hypothesis: two-sided

Example: bulbs1500

databulbs15 <- scan("bulbs1500.txt")
psi.lks.exp.test(databulbs15)
## 
##  One-sample Lilliefors test for exponential distribution
## 
## data:  databulbs15
## Dn.Lillie.exp = 0.25759, p-value = 0.207
## alternative hypothesis: two-sided
psi.lks.exp.test(databulbs15)
## 
##  One-sample Lilliefors test for exponential distribution
## 
## data:  databulbs15
## Dn.Lillie.exp = 0.25759, p-value = 0.221
## alternative hypothesis: two-sided
psi.lks.exp.test(databulbs15, Nsim=10000)
## 
##  One-sample Lilliefors test for exponential distribution
## 
## data:  databulbs15
## Dn.Lillie.exp = 0.25759, p-value = 0.2156
## alternative hypothesis: two-sided
# example: bulbs: is this the same as bulbs1000?
#
bulbs
##  [1] 1615.3880 1751.3540  951.2327 3727.3430 1333.2010  914.8320  507.4933
##  [8]  213.3106  862.1596 2217.3740
mean(bulbs)
## [1] 1409.369
ks.test(bulbs, pexp, rate = 1/1500)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  bulbs
## D = 0.23717, p-value = 0.5504
## alternative hypothesis: two-sided
ks.test(bulbs, pexp, rate = 1/1000)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  bulbs
## D = 0.37775, p-value = 0.08623
## alternative hypothesis: two-sided

Carry out Lilliefors test (simulation is used, so slight differences in repeated calculation)

## 
##  One-sample Lilliefors test for exponential distribution
## 
## data:  bulbs
## Dn.Lillie.exp = 0.25759, p-value = 0.221
## alternative hypothesis: two-sided
## 
##  One-sample Lilliefors test for exponential distribution
## 
## data:  bulbs
## Dn.Lillie.exp = 0.25759, p-value = 0.222
## alternative hypothesis: two-sided
psi.lks.exp.test(bulbs, Nsim = 10000)   # for more precision
## 
##  One-sample Lilliefors test for exponential distribution
## 
## data:  bulbs
## Dn.Lillie.exp = 0.25759, p-value = 0.2223
## alternative hypothesis: two-sided

(semi-)diy (full diy would also calc. the Dn stat. by diy)

z <- bulbs/mean(bulbs)
zDn <- psi.Dn(z, pexp, rate=1)

crit. value at alpha=0.05

DnN0p05 <- psi.qlks.exp(1-0.05, length(z))

or, for more precision,

DnN0p05 <- psi.qlks.exp(1-0.05, length(z), Nsim=10000)

zDn > DnN0p05
##  0.95 
## FALSE
# p-value
1 - psi.plks.exp(zDn, length(z), Nsim=10000)
## 0.257590782926558 
##            0.2234

Example: Oxboys (needs clean-up)

library(mlmRev)
## Loading required package: lme4
## Loading required package: Matrix
summary(Oxboys)          # Oxboys are from library(mlmRev)
##     Subject         age               height         Occasion 
##  1      :  9   Min.   :-1.00000   Min.   :126.2   1      :26  
##  10     :  9   1st Qu.:-0.46300   1st Qu.:143.8   2      :26  
##  11     :  9   Median :-0.00270   Median :149.5   3      :26  
##  12     :  9   Mean   : 0.02263   Mean   :149.5   4      :26  
##  13     :  9   3rd Qu.: 0.55620   3rd Qu.:155.5   5      :26  
##  14     :  9   Max.   : 1.00550   Max.   :174.8   6      :26  
##  (Other):180                                      (Other):78
Oxboys[1:5,]
##   Subject     age height Occasion
## 1       1 -1.0000  140.5        1
## 2       1 -0.7479  143.4        2
## 3       1 -0.4630  144.8        3
## 4       1 -0.1643  147.1        4
## 5       1 -0.0027  147.7        5
Oxboys[1:5, "height"]
## [1] 140.5 143.4 144.8 147.1 147.7
dataoxheight <- Oxboys[,"height"]
plot(dataoxheight)

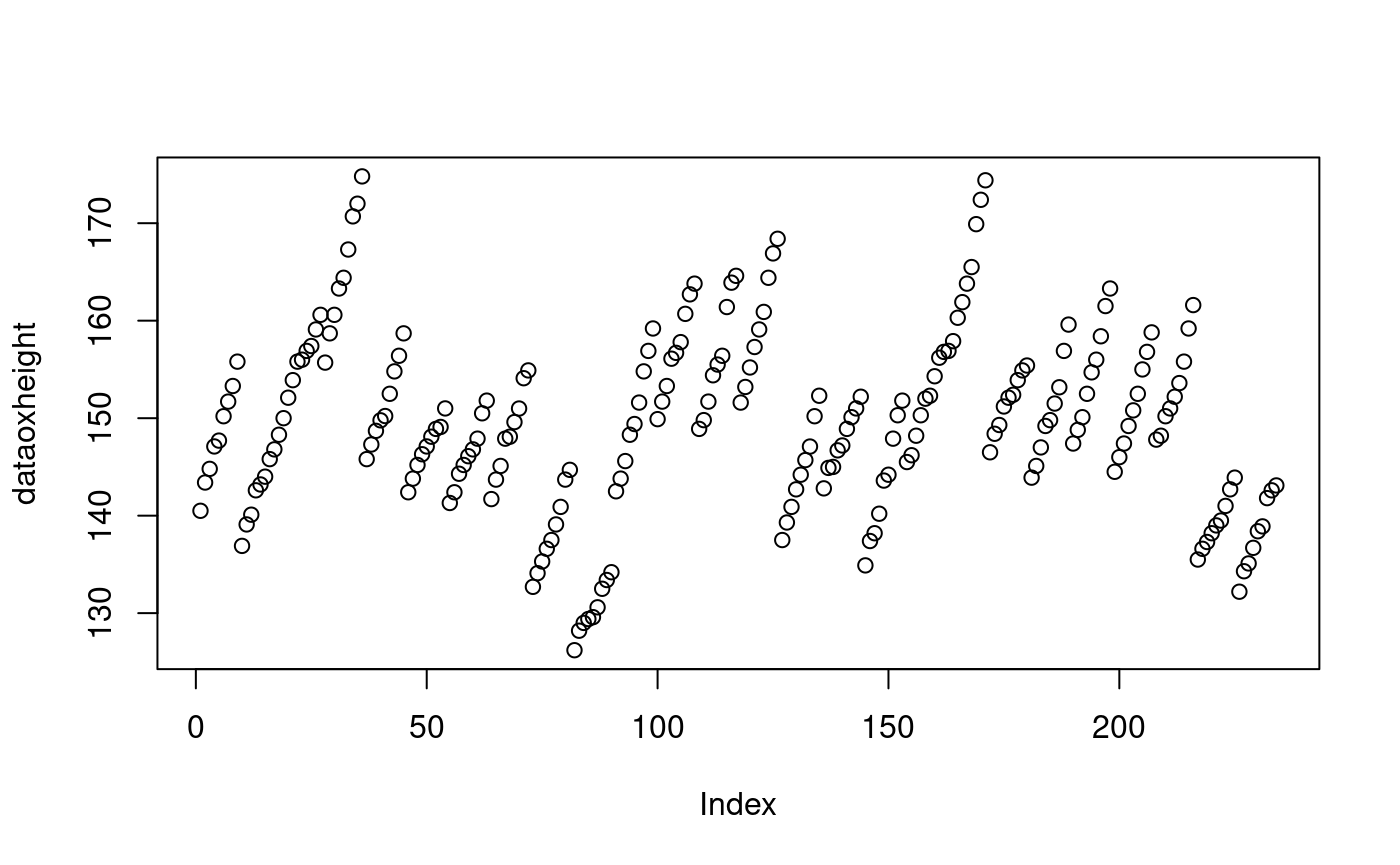
summary(dataoxheight)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   126.2   143.8   149.5   149.5   155.5   174.8
hist(dataoxheight, freq=FALSE)  # todo: overlay exp pdf?

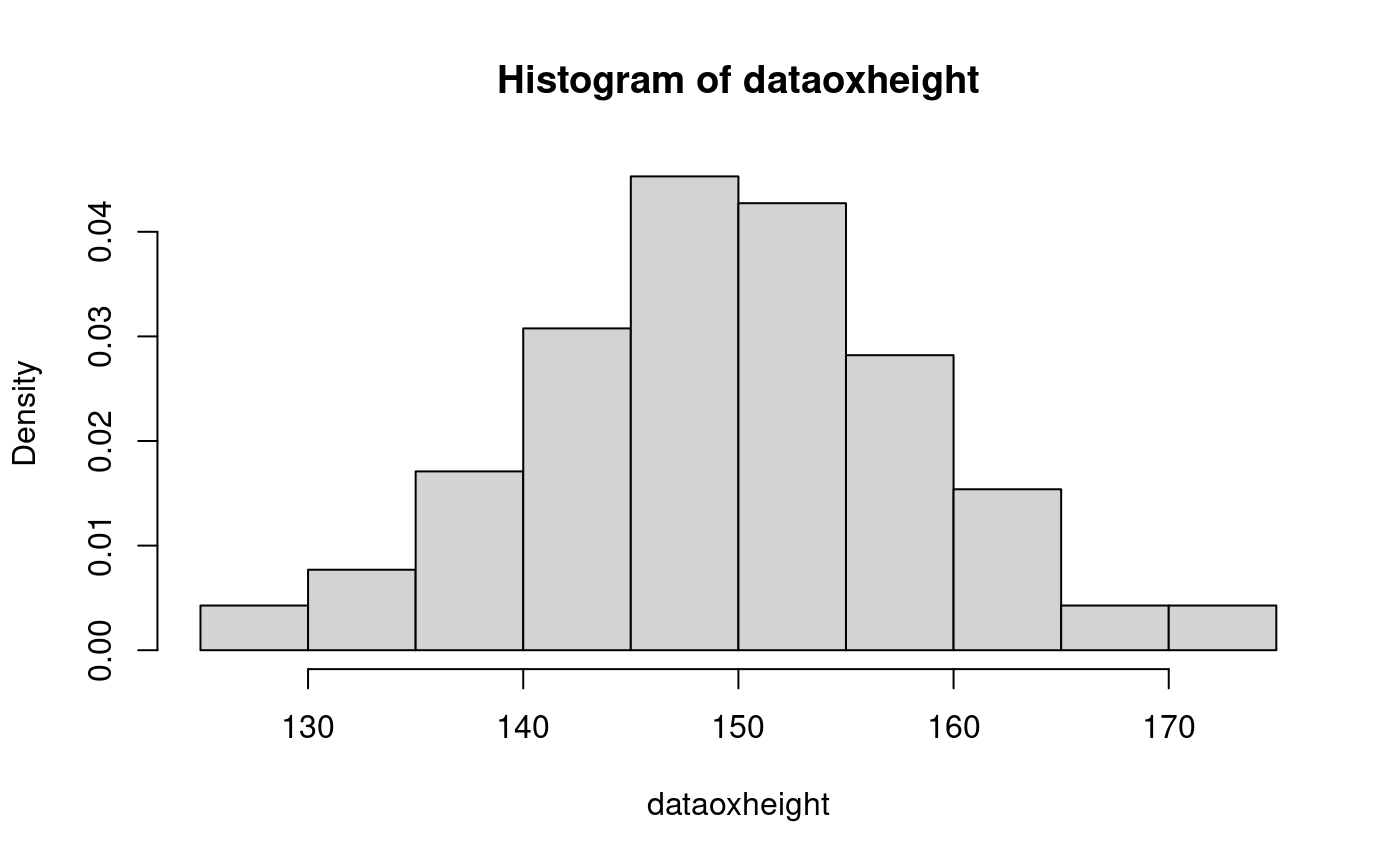
boxplot(dataoxheight)

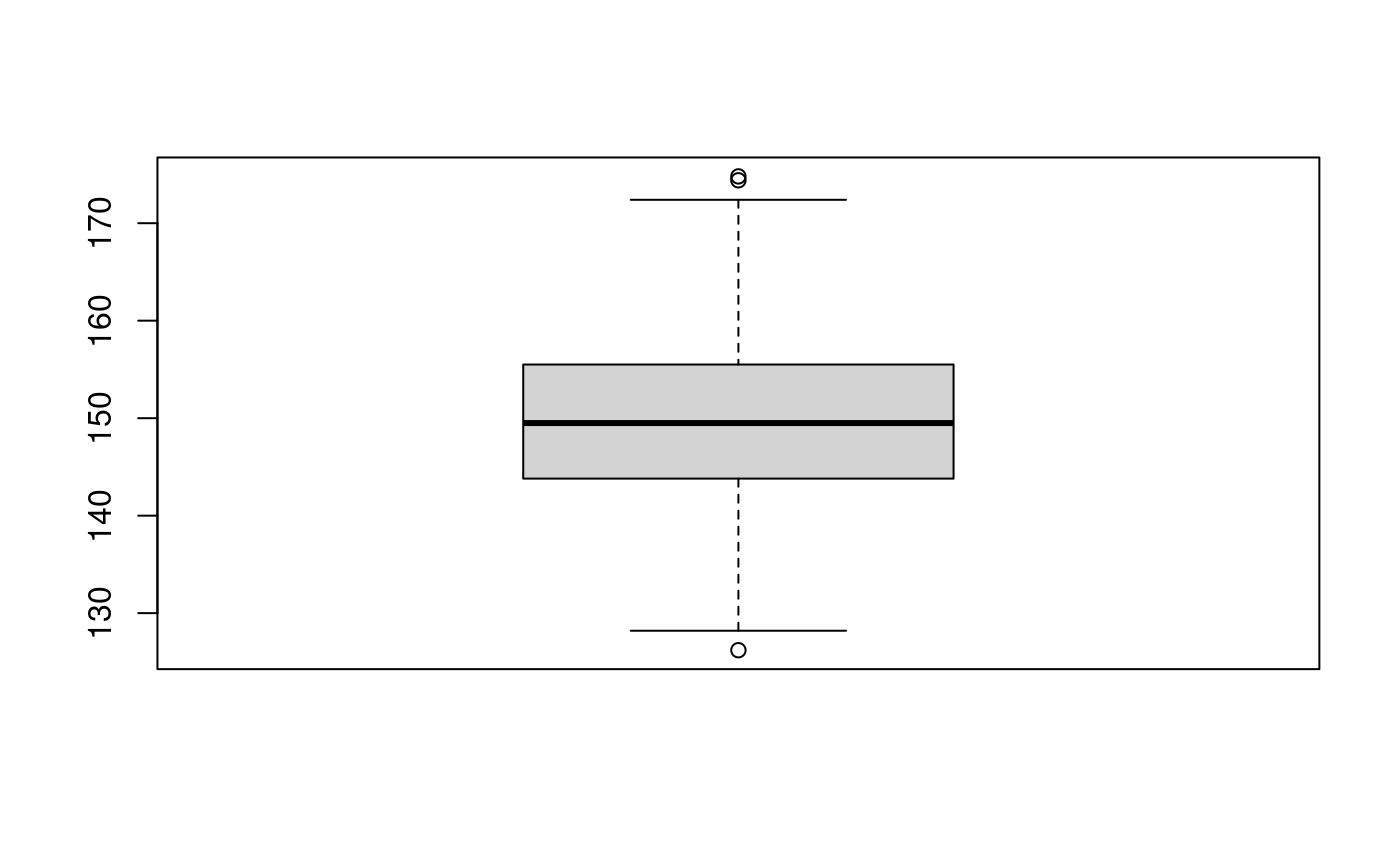
qqnorm(dataoxheight)

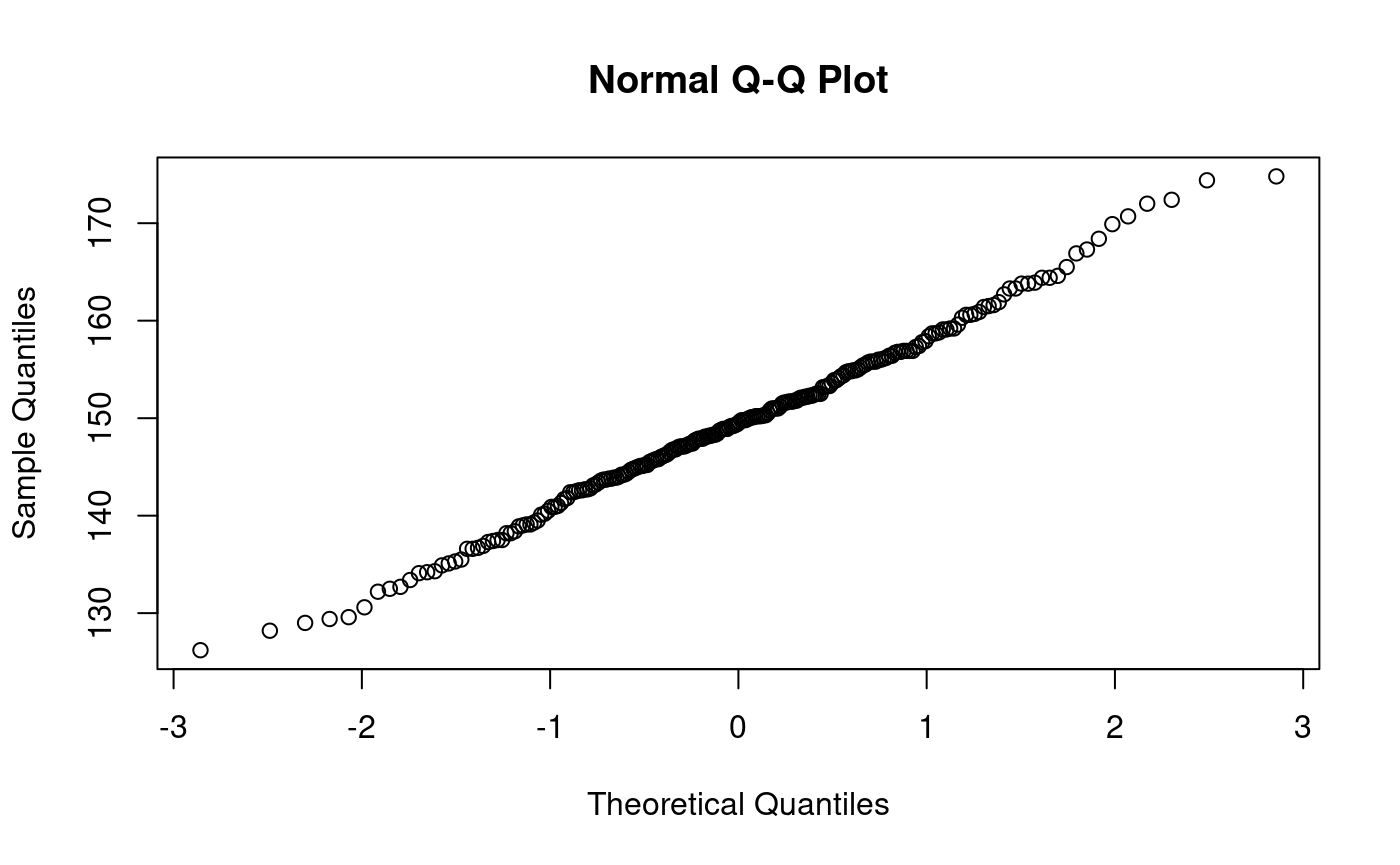
library(nortest)
lillie.test(dataoxheight)
## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  dataoxheight
## D = 0.042614, p-value = 0.378
ks.test(dataoxheight, pnorm, mean=mean(dataoxheight), sd=sd(dataoxheight)) # for comparison
## Warning in ks.test(dataoxheight, pnorm, mean = mean(dataoxheight), sd =
## sd(dataoxheight)): ties should not be present for the Kolmogorov-Smirnov test
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  dataoxheight
## D = 0.042614, p-value = 0.7891
## alternative hypothesis: two-sided
ks.test(unique(dataoxheight), "pnorm", mean=mean(dataoxheight), sd=sd(dataoxheight))
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  unique(dataoxheight)
## D = 0.043867, p-value = 0.8932
## alternative hypothesis: two-sided
# add some jitter to remove ties;  ?psi.jitter
# ?psi.jitter
ks.test(psi.jitter(dataoxheight,amount=0.5), pnorm, mean=mean(dataoxheight), sd=sd(dataoxheight))
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  psi.jitter(dataoxheight, amount = 0.5)
## D = 0.035408, p-value = 0.931
## alternative hypothesis: two-sided
ks.test(psi.jitter(dataoxheight,amount=0.5), pnorm, mean=mean(dataoxheight), sd=sd(dataoxheight))
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  psi.jitter(dataoxheight, amount = 0.5)
## D = 0.030803, p-value = 0.9795
## alternative hypothesis: two-sided
#?psi.Dn
psi.Dn(dataoxheight, pnorm, mean=mean(dataoxheight), sd=sd(dataoxheight), ties.jitter=TRUE)
## [1] 0.04111807
# ?psi.jitter
any(duplicated(dataoxheight))
## [1] TRUE
xj <- psi.jitter(dataoxheight, 0.5)
any(duplicated(xj))
## [1] FALSE
ks.test(xj, "pnorm", mean=mean(dataoxheight), sd = sd(dataoxheight))
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  xj
## D = 0.045339, p-value = 0.7219
## alternative hypothesis: two-sided
###########################################

datamig
##  [1]  98  90 155  86  80  84  70 128  93  40 108  90 130  48  55 106 145 126 100
## [20] 115  75  95  38  66  63  32 105 118  21 142
ls(pattern="data*")
## [1] "databarbi"    "databulbs"    "databulbs15"  "datamig"      "datamoths"   
## [6] "dataoxheight" "datasales"
databarbi
##  [1] 2.70 2.20 2.80 0.90 0.30 4.30 6.20 1.25 0.90 0.60 3.00 1.60 3.20 4.10 0.79
## [16] 3.90 0.72 1.30 7.70 2.50 1.10 6.70 1.70 3.50 5.10 1.66 2.00 3.70 1.12 0.64
## [31] 2.80 6.10
databulbs
##  [1]  730 1648 1321  319  696   21  192  780 1659  167

Example: checking normality of residuals from lm()

datamilk <-
   data.frame(
     x = c(42.7,40.2,38.2,37.6,32.2,32.2,28,27.2,26.6,23,22.7,21.8,21.3,20.2),
     y = c(1.2,1.16,1.07,1.13,0.96,1.07,0.85,0.87,0.77,0.74,0.76,0.69,0.72,0.64)
   )
fitmilk <- lm(y~x, data=datamilk)
datamilk
##       x    y
## 1  42.7 1.20
## 2  40.2 1.16
## 3  38.2 1.07
## 4  37.6 1.13
## 5  32.2 0.96
## 6  32.2 1.07
## 7  28.0 0.85
## 8  27.2 0.87
## 9  26.6 0.77
## 10 23.0 0.74
## 11 22.7 0.76
## 12 21.8 0.69
## 13 21.3 0.72
## 14 20.2 0.64
fitmilk
## 
## Call:
## lm(formula = y ~ x, data = datamilk)
## 
## Coefficients:
## (Intercept)            x  
##     0.17558      0.02458
summary(fitmilk)
## 
## Call:
## lm(formula = y ~ x, data = datamilk)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.059293 -0.024055 -0.005221  0.024711  0.103082 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.175576   0.046399   3.784   0.0026 ** 
## x           0.024576   0.001523  16.139 1.68e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.04203 on 12 degrees of freedom
## Multiple R-squared:  0.956,  Adjusted R-squared:  0.9523 
## F-statistic: 260.5 on 1 and 12 DF,  p-value: 1.678e-09
# plot(fitmilk)
resfitmilk <- residuals(fitmilk)
lillie.test(resfitmilk)
## 
##  Lilliefors (Kolmogorov-Smirnov) normality test
## 
## data:  resfitmilk
## D = 0.15457, p-value = 0.4848

todo: also qq-plot? ## Lilliefors test for exponentiality

?psi.plks
?psi.plks.exp
?psi.lks.exp.test
?psi.Dn
?psi.pks
databulbs <- scan("bulbs1000.txt")
ks.test(databulbs, "pexp", rate=2)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  databulbs
## D = 1, p-value < 2.2e-16
## alternative hypothesis: two-sided
mean(databulbs)
## [1] 753.3
1/mean(databulbs)
## [1] 0.001327492
ks.test(databulbs, "pexp", rate=1/1000)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  databulbs
## D = 0.19033, p-value = 0.7978
## alternative hypothesis: two-sided
psi.plks.exp(0.203, df = length(databulbs))
## 0.203 
##  0.49
1 - psi.plks.exp(0.203, df = length(databulbs))
## 0.203 
## 0.549
curve(psi.pks(x,length(databulbs)), from=0, to=1)
curve(psi.plks.exp(x,length(databulbs)), from=0, to=1, col="blue", add=TRUE)
abline(h=0.95)

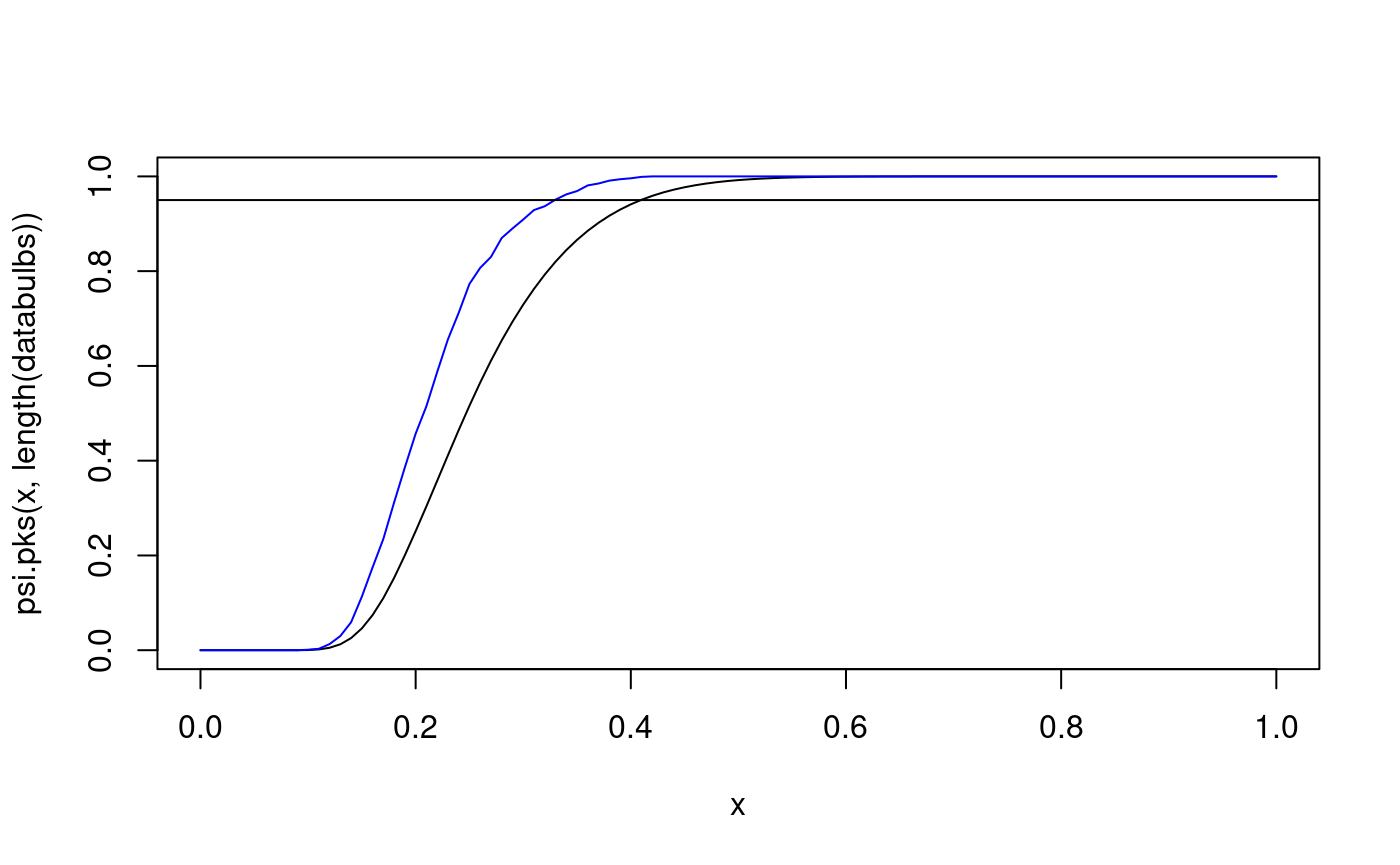
# ?names
# ?c
databulbs
##  [1]  730 1648 1321  319  696   21  192  780 1659  167
ks.test(databulbs, "pexp", rate=1/1000)
## 
##  One-sample Kolmogorov-Smirnov test
## 
## data:  databulbs
## D = 0.19033, p-value = 0.7978
## alternative hypothesis: two-sided
psi.Dn(databulbs, "pexp", rate=1/1000)
## [1] 0.1903292

q : P(Dn < q) = 0.95 for selected values of n

psi.pks(0.6239385,     4)
## [1] 0.95
psi.pks(0.2940753,    20)
## [1] 0.95
psi.pks(0.1340279,   100)
## [1] 0.95
psi.pks(0.04294685, 1000)   # asymptotic approximation
## [1] 0.95
databulbs
##  [1]  730 1648 1321  319  696   21  192  780 1659  167
psi.lks.exp.test(databulbs)
## 
##  One-sample Lilliefors test for exponential distribution
## 
## data:  databulbs
## Dn.Lillie.exp = 0.20305, p-value = 0.533
## alternative hypothesis: two-sided
length(databulbs)
## [1] 10
psi.plks.exp(0.203, df=10)
## 0.203 
## 0.478
1 - psi.plks.exp(0.203, df=10)
## 0.203 
##  0.54